A block of weight 100N lying on a horizontal surface just beging to when a horizontal to move when a horinzontal force of 25N acts on it Determine the coefficent of static friction
To determine the coefficient of static friction (μ) for the block, we can follow these steps:
1. Identify the Forces Acting on the Block:
- The weight of the block (W) is given as 100 N, acting vertically downward.
- The normal force (N) acting on the block is equal to its weight since the block is on a horizontal surface, so N = W = 100 N.
- A horizontal force (F) of 25 N is applied to the block, which is just enough to overcome static friction and initiate movement.
2. Understand the Concept of Limiting Friction:
- The force of static friction (f_s) that opposes the motion of the block can be expressed as:
fs=μs⋅N
- Here, μ_s is the coefficient of static friction, and N is the normal force.
3. Set Up the Equation:
- At the point just before the block starts to move, the applied force (F) is equal to the maximum static friction force (f_s):
F=fs
- Substituting the expression for static friction, we have:
25N=μs⋅100N
4. Solve for the Coefficient of Static Friction (μ_s):
- Rearranging the equation to solve for μ_s:
μs=FN=25N100N
- Simplifying this gives:
μs=14=0.25
5. Conclusion:
- The coefficient of static friction (μ_s) for the block is 0.25.
- The weight of the block (W) is given as 100 N, acting vertically downward.
- The normal force (N) acting on the block is equal to its weight since the block is on a horizontal surface, so N = W = 100 N.
- A horizontal force (F) of 25 N is applied to the block, which is just enough to overcome static friction and initiate movement.
- The force of static friction (f_s) that opposes the motion of the block can be expressed as:
fs=μs⋅N
- Here, μ_s is the coefficient of static friction, and N is the normal force.
- At the point just before the block starts to move, the applied force (F) is equal to the maximum static friction force (f_s):
F=fs
- Substituting the expression for static friction, we have:
25N=μs⋅100N
- Rearranging the equation to solve for μ_s:
μs=FN=25N100N
- Simplifying this gives:
μs=14=0.25
- The coefficient of static friction (μ_s) for the block is 0.25.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
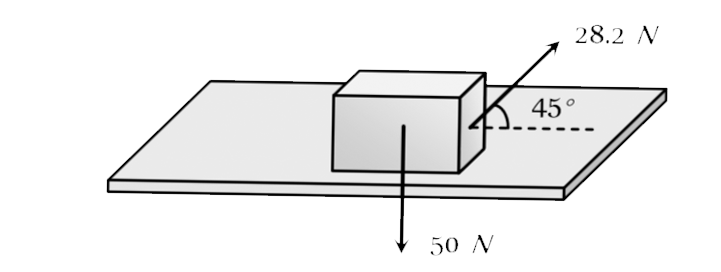
A body of weight 50 N placed on a horizontal surface is just moved by a force of 28.2 N. the frictional force and the narmal reaction are
View SolutionA block of weight 100N is lying on a rough horizontal surface. If coefficient of friction 1/√3. The least possible force that can move the block is
View Solution
Knowledge Check
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
A10ms−2B5ms−2C15ms−2D0.5ms−2
A block of weight 200N is pulled along a rough horizontal surface at constant speed by a force 100N acting at an angle 30∘ above the horizontal. The coefficient of friction between the block and the surface is
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the block will be.
View SolutionA block lying on an inclined plane has a weigh of 50N .It just beings to side down when inclination of plane with the horizontal is 30∘ find the coefficient of static plane friction .
View SolutionA block is in limiting equilibrium on a rough horizontal surface. If the net contact force is √3 times the normal force, the coefficient of static friction is
View SolutionA body of weight 20N is on a horizontal surface, minimum force applied to pull it when applied force makes an angle 60° with horizontal (angle of friction a = 30°) is
View Solution
