An engine of power 58.8kW pulls a train of mass 2×105kg with a velocity of 36kmh−1. The coefficient of kinetic friction is
0.3
0.03
0.003
0.0003
The correct Answer is:C
To solve the problem, we need to find the coefficient of kinetic friction (μk) acting on a train being pulled by an engine. Here are the steps to arrive at the solution:
Step 1: Convert the velocity from km/h to m/s
The velocity of the train is given as 36km/h. We need to convert this to meters per second (m/s).
Velocity=36km/h×1000m1km×1h3600s=10m/s
Step 2: Write down the power equation
The power generated by the engine is given as 58.8kW, which can be converted to watts:
Power=58.8kW=58.8×103W
Step 3: Relate power to frictional force
Since the train is moving at a constant velocity, the power generated by the engine is used to overcome the frictional force. The power due to friction can be expressed as:
Power=Friction Force×Velocity
Step 4: Express the friction force
The friction force (Fk) can be expressed in terms of the coefficient of kinetic friction (μk) and the normal force. The normal force for the train is equal to its weight:
Fk=μk⋅(m⋅g)
Where:
- m=2×105kg (mass of the train)
- g=9.8m/s2 (acceleration due to gravity)
Step 5: Substitute the values into the power equation
Now substituting the expression for friction force into the power equation:
58.8×103=μk⋅(2×105⋅9.8)⋅10
Step 6: Solve for μk
Rearranging the equation to isolate μk:
μk=58.8×103(2×105⋅9.8)⋅10
Calculating the denominator:
2×105⋅9.8⋅10=19.6×106
Now substituting back into the equation for μk:
μk=58.8×10319.6×106=58.819.6×10−3
Calculating 58.819.6:
58.819.6=3
Thus,
μk=3×10−3=0.003
Final Answer
The coefficient of kinetic friction (μk) is 0.003.
---
The velocity of the train is given as 36km/h. We need to convert this to meters per second (m/s).
The power generated by the engine is given as 58.8kW, which can be converted to watts:
Since the train is moving at a constant velocity, the power generated by the engine is used to overcome the frictional force. The power due to friction can be expressed as:
The friction force (Fk) can be expressed in terms of the coefficient of kinetic friction (μk) and the normal force. The normal force for the train is equal to its weight:
- m=2×105kg (mass of the train)
- g=9.8m/s2 (acceleration due to gravity)
Now substituting the expression for friction force into the power equation:
Rearranging the equation to isolate μk:
The coefficient of kinetic friction (μk) is 0.003.
Similar Questions
A 10 metric ton truck drives up a hilly road of gradient 1 in 50 at a speed of 36kmh−1 if the coefficient of kinetic friction between the road and tyres is 0.2, calculate the power delivered by the engine (g=10ms−2)
View SolutionA 10 metric ton truck drives up a hilly road of gradient 1 in 50 at a speed of 36kmh−1 if the co-efficient of kinetic friction between the road and tyres is 0.2, calculate the power delivered by the engine (g=10ms−2)
View SolutionAn engine of one metric ton is going up an inclined plane, 1 in 2 at the rate of 36 kmph. If the coefficient of friction is 1/√3 , the power of engine is
View SolutionDetermine the acceleration of the 5kg block A . Neglect the mass of the pulley and cords . The block B has a mass of 10kg, The coefficient of kinetic friction between block B and the surface is μk=0.1 (take g=10m/s2)
 View Solution
View SolutionTwo blocks are connected over a massless pulley as shown in figure. The mass of block A is 10 kg and the coefficient of kinetic friction is 0.2 Block A sliders down the incline at constant speed. The mass of block B in kg is
 View Solution
View SolutionA block of mass 10kg is dragged across a horizontal surface by pulling the block with force of 100N. The force is applied by attaching a chord to the block. The chord is inclined at an angle of 60∘ with the horizontal. If the coefficient of kinetic friction is 0.2 what is the acceleration of the block ?
View SolutionA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
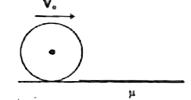 View Solution
View SolutionBlock of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-
View SolutionA block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and surface is 0.5. Tension in the cord is (take, g=9.8ms−2)
 View Solution
View SolutionConsider a horizontal surface moving vertically upward with velocity 2ms−1. A small ball of mass 2 kg is moving with velocity (2ˆi−2ˆj)ms−1 If the coefficient of restitution and coefficient of friction are 12and13 respectively, find the horizontal velocity (in ms−1) of the ball after the collision.
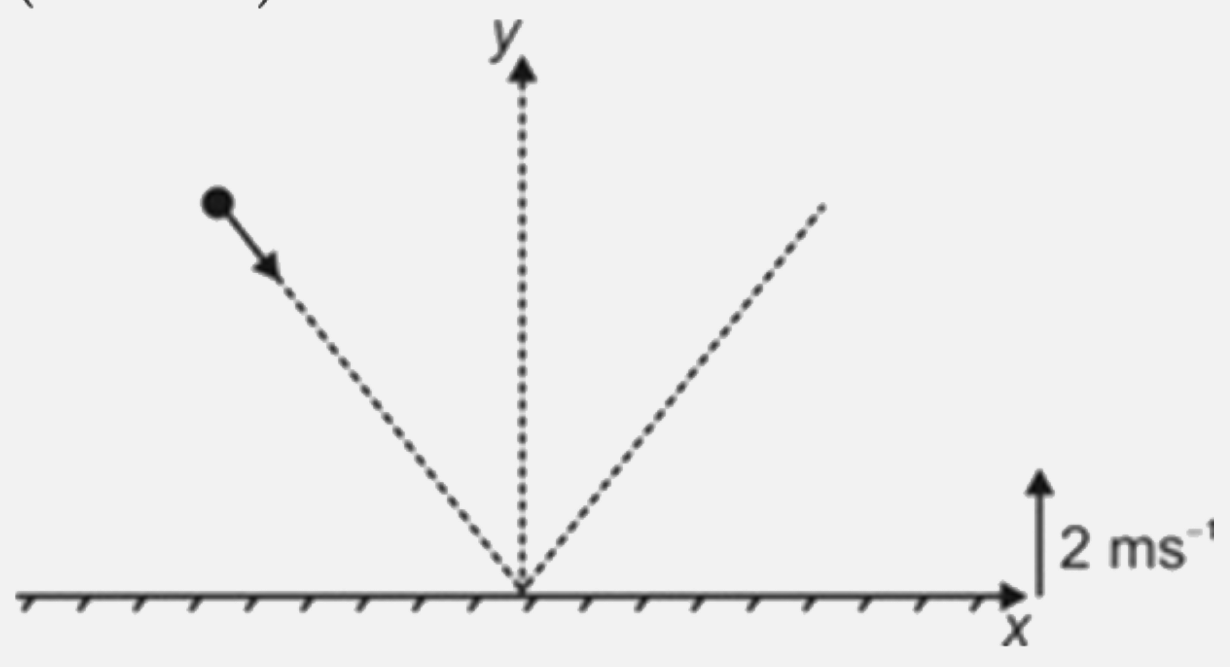 View Solution
View Solution

