A ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
the linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkg
the gain in kinetic energy is mv208
the loss in kinetic energy is mv204
the work done by friction force is −3mv208
The correct Answer is:C
Step by step video & image solution for A ring of mass m sliding on a smooth surface with velocity v_(0) enters rough surface with coefficient of kinetic friction mu_(k), then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
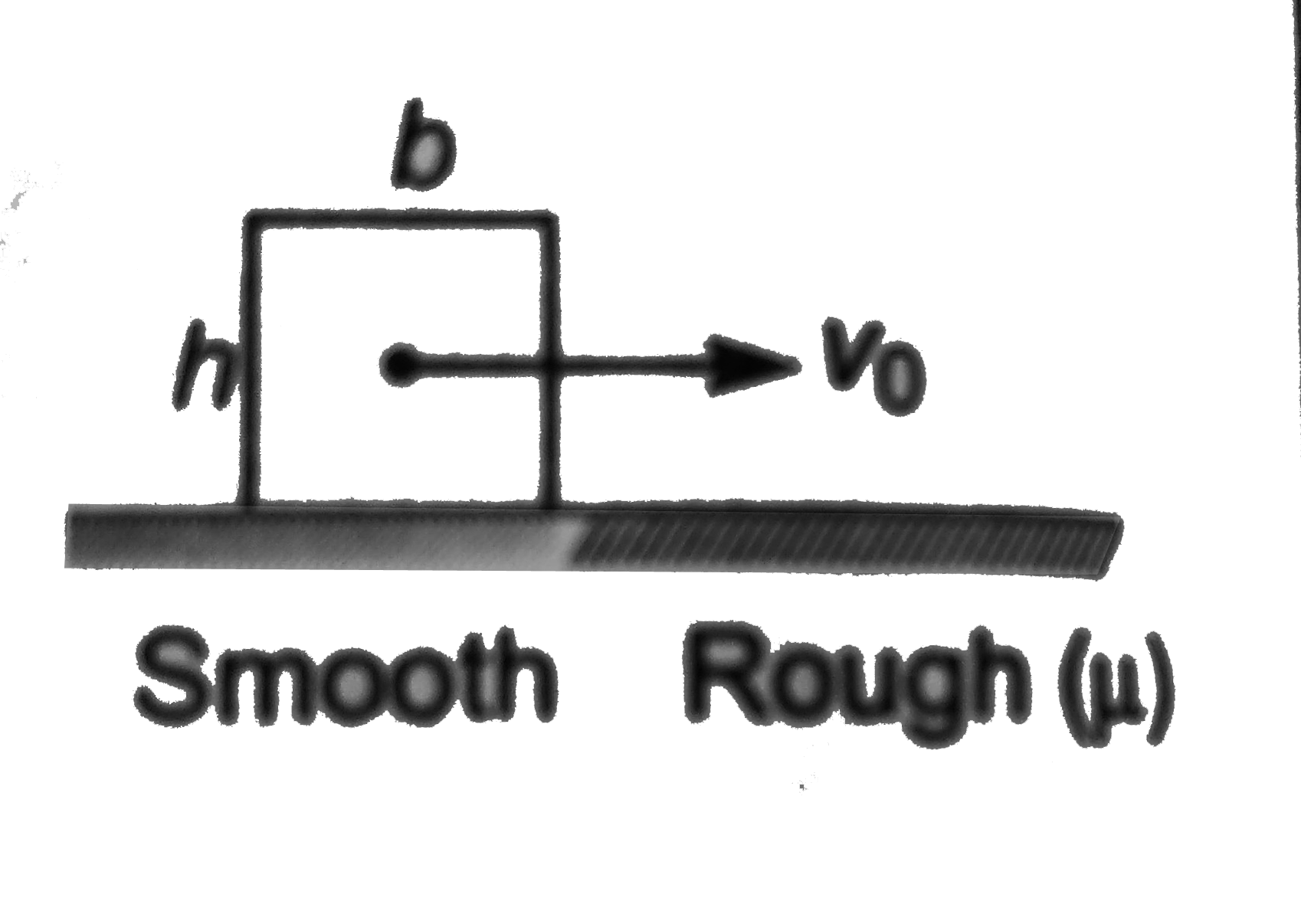
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.
View SolutionA block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

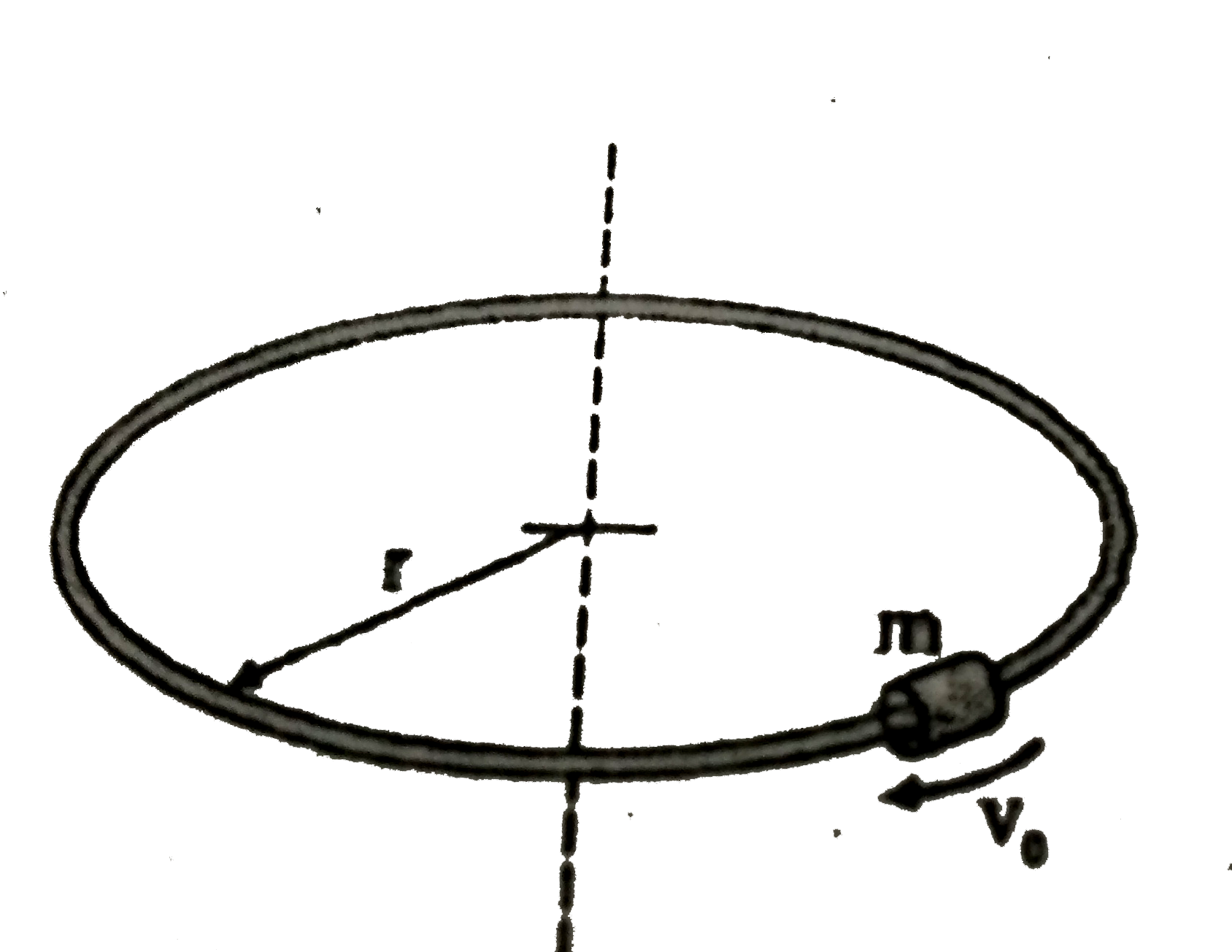
View SolutionA small hoop of mass m is given an initial velocity of magnitude v0 on the horizontal circular ring of radius 'r'. If the coefficient of kinetic friction is μk the tangential acceleration of the hoop immediately after is release is ( assume the horizontal ring to be fixed and not in contact with any supporting surface )
View SolutionA heavy chain with a mass per unite length p is pulled by the constant force F along a horizental surface consisting of a smooth section and a rough section. The chain is initially at rest on the rough surface with x=0 . If the coefficient of kinetic friction between the chain and the rough surface is μk determine the velocity v of the chain when x=L . The force F is hreater than μkogL in under to initate the motion ,

View SolutionA uniform ring of mass m is placed on a rough horizontal fixed surface as shown in the figure. The coefficient of friction between the left part of the ring and left part of the horizontal surface is μ1=0.6π and between right half and the surface is μ2=0.2π. At the instant shown, now the ring has been imparted an angular velocity in clockwise sense in the figure shown. At this moment magnitude of acceleration of centre O of the ring (in m/s2) is (take g=10m/s2)

View SolutionTwo blocks of equal masses are connected by an ideal string passing over an ideal pulley as shown in the figure
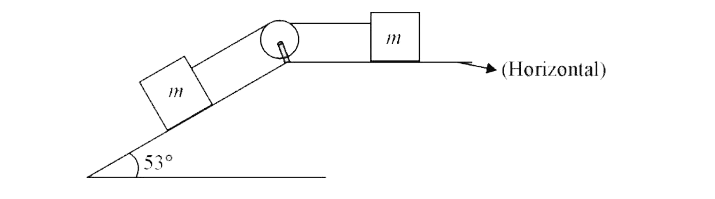
All the surfaces in contact with blocks are rough having coefficient of kinetic friction μ between them. If the blocks slide with constant velocity, find the value of μ
View Solution
