A telephone wire of length 200km has a capacitance of 0.014μFperkm. If it carries an AC of frequency 5kHz what should be the value of an inductor required to be connected in series so that impedence of the circuit is minimum ?
(a)0.35 mH
(b)3.5 mH
(c)2.5 mH
(d)zero
The correct Answer is:A
To solve the problem step by step, we need to find the value of the inductor required to minimize the impedance of the circuit. Let's break down the solution:
Step 1: Calculate the total capacitance of the telephone wire
The capacitance per kilometer is given as 0.014μF/km and the length of the wire is 200km.
Ctotal=Capacitance per km×Length of the wire
Ctotal=0.014μF/km×200km=2.8μF
Step 2: Convert capacitance to farads
Since 1μF=10−6F, we convert Ctotal to farads:
Ctotal=2.8μF=2.8×10−6F
Step 3: Calculate the angular frequency
The frequency f is given as 5kHz. We need to convert this to hertz:
f=5kHz=5×103Hz
Now, calculate the angular frequency ω:
ω=2πf=2π(5×103)≈31415.93rad/s
Step 4: Set the condition for minimum impedance
For minimum impedance, the inductive reactance XL must equal the capacitive reactance XC:
XL=XC
Where:
XL=ωLandXC=1ωC
Thus, we have:
ωL=1ωC
Step 5: Solve for inductance L
Rearranging the equation gives:
L=1ω2C
Step 6: Substitute the values into the equation
Substituting ω and Ctotal:
L=1(31415.93)2×(2.8×10−6)
Step 7: Calculate L
Calculating the denominator:
(31415.93)2≈9.8696×108
Now substituting:
L=19.8696×108×2.8×10−6≈12765.888≈0.0003624H
Step 8: Convert to milliHenries
L≈0.3624mH≈0.35mH
Final Answer
The required inductance L is approximately 0.35mH.
---
The capacitance per kilometer is given as 0.014μF/km and the length of the wire is 200km.
Ctotal=0.014μF/km×200km=2.8μF
Since 1μF=10−6F, we convert Ctotal to farads:
Ctotal=2.8μF=2.8×10−6F
The frequency f is given as 5kHz. We need to convert this to hertz:
f=5kHz=5×103Hz
Now, calculate the angular frequency ω:
ω=2πf=2π(5×103)≈31415.93rad/s
For minimum impedance, the inductive reactance XL must equal the capacitive reactance XC:
XL=XC
Where:
XL=ωLandXC=1ωC
Thus, we have:
ωL=1ωC
Rearranging the equation gives:
L=1ω2C
Substituting ω and Ctotal:
L=1(31415.93)2×(2.8×10−6)
Calculating the denominator:
(31415.93)2≈9.8696×108
Now substituting:
L=19.8696×108×2.8×10−6≈12765.888≈0.0003624H
L≈0.3624mH≈0.35mH
The required inductance L is approximately 0.35mH.
Similar Questions
A 200 km telephone wire has capacity of 0.014μFkm−1. If it carries an alternating current oif frequency 50kHz, what should be the value of an inductance required to be connected in series so that impedance is minimumn ?
View SolutionThe diode used in the circuit shown in the adjacent figure has a constant voltage drop of 0.5V at all currents and a maximum power rating of 100mW.What should be the value of resistor R connected in series with the diode for obtaining maximum current?
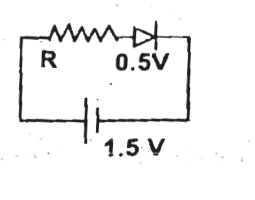 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The diode used in the circuit shown in the figure has a constant voltage drop of 0.5V at all currents and a maximum power rating fo 100 milliwatts. What should be the value of the resistor R, connected in series with the diode for obtaining maximum current?
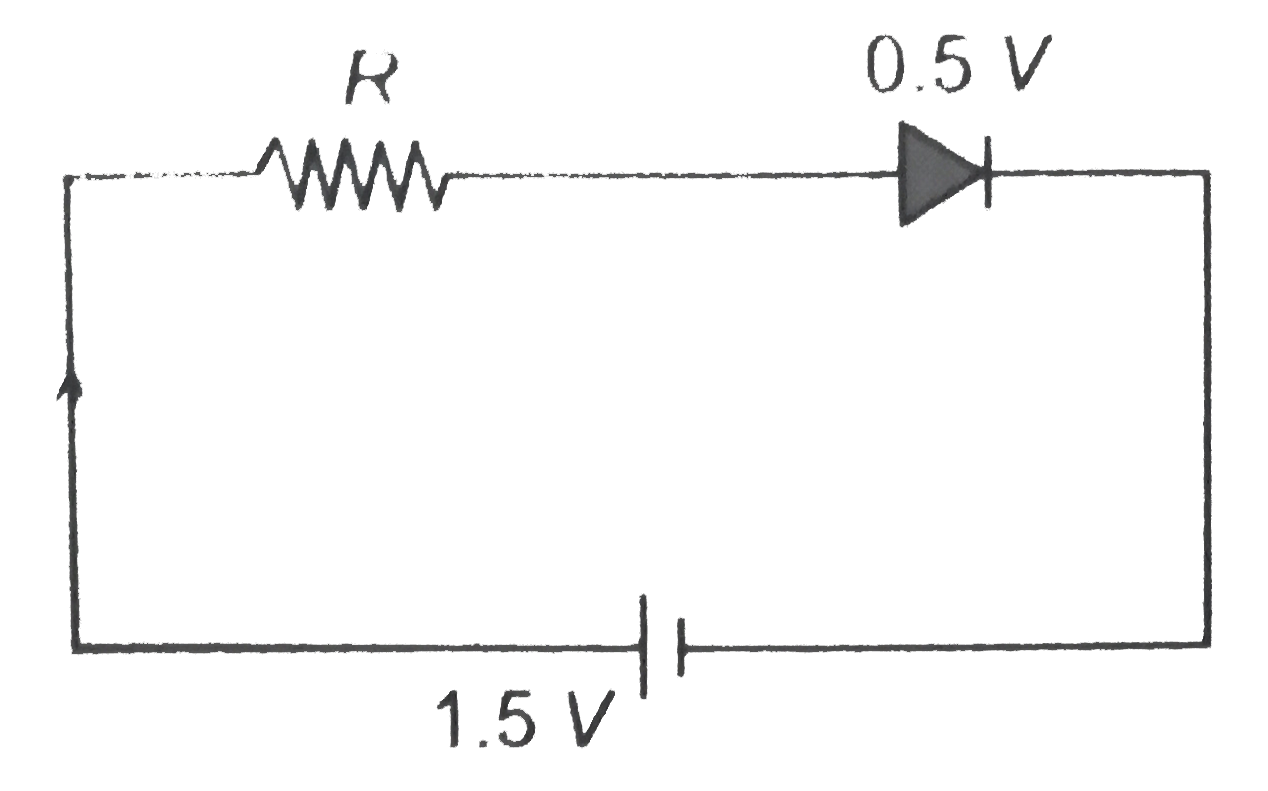 A6.76ΩB20ΩC5ΩD5.6Ω
A6.76ΩB20ΩC5ΩD5.6Ω
An inductor of inductance 100mH is connected in series with a resistance, a variable capacitance and an AC source of frequency 2.0kHz. What should be the value of the capacitance so that maximum current may be drawn into the circuit?
View SolutionIf resistance R =10Ω, inductance L = 2 mH and capacitance C=5μF are connected in series to an AC source of frequency 50 Hz, then at resonance the impedance of circuit is
View SolutionWhen a diode is forward biased, it has a voltage drop of 0.5 V. The safe limit of current through the diode is 10 mA. If a battery of emf 1.5 V is used in the circuit, the value of minimum resistance to be connected in series with the diode so that the current does not exceed the safe limit is :
View SolutionAn L−C−R series circuit with L=0.120H,R=240a, and C=7.30μF carries an rms current of 0.450A with a frequency of 400Hz.
(a) What are the phase angle and power factor for this circuit?
(b) What is the impedance of the circuit?
(c) What is the rms voltage of the source?
(d) What average power is delivered by the source?
(e) What is the average rate at which electrical energy is converted to thermal energy in the resistor?
(f) What is the average rate at which electrical energy is dissipated ( converted to other forms) in the capacitor?
(g) In the inductor ?View SolutionIt is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V Box P contains a capacitance of 1μF in series with a resistance of 32Ω. And the box Q has a coil of self-inductance 4.9mH and a resistance of 68Ωin series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental set up and the reading by him at various moment, answer the following questions.
Impedance of box P at the above frequency isView SolutionIt is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V Box P contains a capacitance of 1μF in series with a resistance of 32Ω. And the box Q has a coil of self-inductance 4.9mH and a resistance of 68Ωin series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental set up and the reading by him at various moment, answer the following questions.
Power factor of the circuit at maximum current isView SolutionAn inductance of 2.0H, a capacitance of 18μF and a resistance of 10kΩ are connected to an AC source of 20V with adjustable frequency. (a) What frequency should be chosen to maximise the current in the circuit? (b) What is the value of this maximum current?
View Solution

