An inductance of 2.0H, a capacitance of 18μF and a resistance of 10kΩ are connected to an AC source of 20V with adjustable frequency. (a) What frequency should be chosen to maximise the current in the circuit? (b) What is the value of this maximum current?
The correct Answer is:(a)2503πHz,(b)2mA
To solve the problem step by step, we will break it down into two parts as given in the question.
Part (a): Finding the Frequency to Maximize Current
1. Identify the given values:
- Inductance L=2.0H
- Capacitance C=18μF=18×10−6F
- Resistance R=10kΩ=10×103Ω
- Voltage V=20V
2. Determine the resonance condition:
- At resonance, the inductive reactance XL equals the capacitive reactance XC.
- The formula for resonance frequency f is given by:
f=12π√LC
3. Substitute the values into the formula:
f=12π√2.0×18×10−6
4. Calculate the value inside the square root:
LC=2.0×18×10−6=36×10−6=3.6×10−5
√LC=√3.6×10−5≈0.006
5. Calculate the frequency:
f=12π×0.006≈10.0377≈26.5Hz
Rounding off, we get:
f≈27Hz
Part (b): Finding the Maximum Current
1. Use Ohm's law to find the maximum current:
- The maximum current I in the circuit can be calculated using:
I=VR
2. Substitute the values:
I=20V10×103Ω=2010000=0.002A
3. Convert to milliampere:
I=2mA
Final Answers:
- (a) The frequency to maximize the current is 27Hz.
- (b) The value of the maximum current is 2mA.
- Inductance L=2.0H
- Capacitance C=18μF=18×10−6F
- Resistance R=10kΩ=10×103Ω
- Voltage V=20V
- At resonance, the inductive reactance XL equals the capacitive reactance XC.
- The formula for resonance frequency f is given by:
f=12π√LC
f=12π√2.0×18×10−6
LC=2.0×18×10−6=36×10−6=3.6×10−5
√LC=√3.6×10−5≈0.006
f=12π×0.006≈10.0377≈26.5Hz
Rounding off, we get:
f≈27Hz
- The maximum current I in the circuit can be calculated using:
I=VR
I=20V10×103Ω=2010000=0.002A
I=2mA
- (a) The frequency to maximize the current is 27Hz.
- (b) The value of the maximum current is 2mA.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-1
14 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-2
6 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS
11 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
Similar Questions
An inductance L , a capacitor of 20μF and a resistor of 10Ω are connected in series with an AC source of frequency 50 Hz . If the current is in phase with the voltage, then the inductance of the inductor is
View SolutionA circuit has a resistance of 11Ω, an inductive reactance of 25Ω, and a capacitive resistance of 18Ω. It is connected to an AC source of 260V and 50Hz. The current through the circuit (in amperes) is
View SolutionAn inductor of inductance 100mH is connected in series with a resistance, a variable capacitance and an AC source of frequency 2.0kHz. What should be the value of the capacitance so that maximum current may be drawn into the circuit?
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
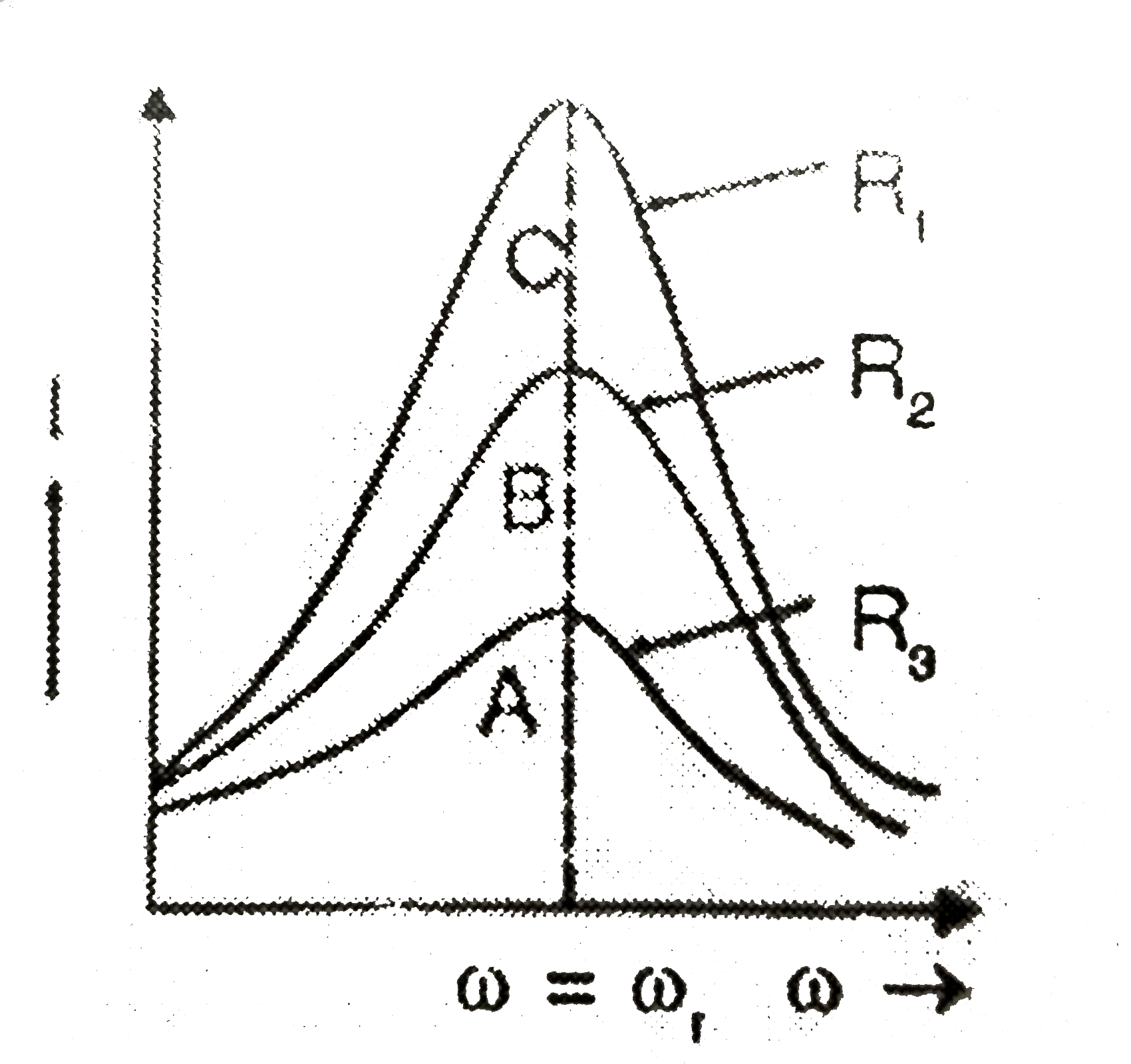
View SolutionA 100μF capacitor in series with a 40Ω resistance is connected to 110 V, 60 Hz supply.
(a) what is the maximum current in the circuit ?
(b) what is the time lag between the current maximum and the voltage maximum ?
View SolutionA coil of resistance 300Ω and inductance 1.0 henry is connected across an voltages source of frequency 300/2πHz. The phase difference between the voltage and current in the circuit is
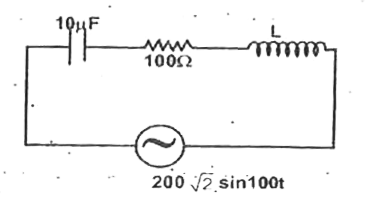
View SolutionA 10 muF capacitor, an inductor and a resistor of 100Omega are connected to an alternating source of emf 200sqrt2 sin 100t as shown in the figure. What is the r.m.s current in the circuit and the value of the inductance if the current and the source voltage attain their maxima simultaneously? What is the average power consumed in this case
View SolutionAn inductive circuit a resistance of 10ohm and an inductance of 2.0 henry. If an AC voltage of 120volt and frequency of 60Hz is applied to this circuit, the current in the circuit would be nearly
View SolutionAn LC circuit (L=0.01H,C=1μF) is connected to an AC source of variable frequency. If the frequency is varied from 1 kHz, then show the consequent variation of impedance by a rough sketch.

View SolutionA capacitor of capacitance 100μF and a coil of resistance 50Ω and inductance 0.5H are connected in series with a110V,50HzAC source. Find the rms value of the current.
View Solution
