Two particles A and B located at points (0,−10√3) and (0,0) in xy plane. They start moving simultaneously at time t=0 with constant velocities →VA=5ˆim/s and →VB=−5√3ˆjm/s, respectively. Time when they are closest to each other is found to be K/2 second. Find K. All distance are given in meter.
The correct Answer is:3
To solve the problem, we need to find the time when the two particles A and B are closest to each other. Let's break down the solution step by step.
Step 1: Define the initial positions and velocities
- Particle A is at position (0,−10√3) and moves with a velocity →VA=5^i m/s.
- Particle B is at position (0,0) and moves with a velocity →VB=−5√3^j m/s.
Step 2: Write the position equations for both particles
The position of particle A at time t can be expressed as:
→rA(t)=(0+5t)^i+(−10√3)^j=5t^i−10√3^j
The position of particle B at time t can be expressed as:
→rB(t)=(0)^i+(0−5√3t)^j=0^i−5√3t^j
Step 3: Find the distance between the two particles
The distance d(t) between the two particles can be calculated using the distance formula:
d(t)=|→rA(t)−→rB(t)|
Substituting the position equations:
d(t)=|(5t^i−10√3^j)−(0^i−5√3t^j)|
=|5t^i+(5√3t−10√3)^j|
=√(5t)2+(5√3t−10√3)2
Step 4: Simplify the distance equation
Calculating the square of the distance:
d2(t)=(5t)2+(5√3t−10√3)2
=25t2+(5√3t−10√3)2
Expanding the second term:
=25t2+(25⋅3)t2−2⋅5√3⋅10√3t+100⋅3
=25t2+75t2−100⋅5+300
=100t2−100√3t+300
Step 5: Find the time when the distance is minimum
To find the minimum distance, we differentiate d2(t) with respect to t and set it to zero:
ddt(100t2−100√3t+300)=200t−100√3=0
Solving for t:
200t=100√3
t=√32
Step 6: Relate time to K
According to the problem, the time when they are closest is given as K2 seconds. Therefore:
K2=√32
Thus, we can find K:
K=√3
Final Answer
The value of K is 3.
- Particle A is at position (0,−10√3) and moves with a velocity →VA=5^i m/s.
- Particle B is at position (0,0) and moves with a velocity →VB=−5√3^j m/s.
The position of particle A at time t can be expressed as:
→rA(t)=(0+5t)^i+(−10√3)^j=5t^i−10√3^j
→rB(t)=(0)^i+(0−5√3t)^j=0^i−5√3t^j
The distance d(t) between the two particles can be calculated using the distance formula:
d(t)=|→rA(t)−→rB(t)|
Substituting the position equations:
d(t)=|(5t^i−10√3^j)−(0^i−5√3t^j)|
=|5t^i+(5√3t−10√3)^j|
=√(5t)2+(5√3t−10√3)2
Calculating the square of the distance:
d2(t)=(5t)2+(5√3t−10√3)2
=25t2+(5√3t−10√3)2
Expanding the second term:
=25t2+(25⋅3)t2−2⋅5√3⋅10√3t+100⋅3
=25t2+75t2−100⋅5+300
=100t2−100√3t+300
To find the minimum distance, we differentiate d2(t) with respect to t and set it to zero:
ddt(100t2−100√3t+300)=200t−100√3=0
Solving for t:
200t=100√3
t=√32
According to the problem, the time when they are closest is given as K2 seconds. Therefore:
K2=√32
Thus, we can find K:
K=√3
The value of K is 3.
Similar Questions
Two particles A and B are located in x−y plane at points (0,0) and (0,4m). They simultaneoulsy start moving with velocities vA=2ˆjm/s and vB=2ˆim/s. Select the correct alternative(s)
View SolutionTwo particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then

View Solution
Knowledge Check
Two identical balls A and B moving with velocities + 0.5 m/s and −0.3.m/s respectively collide head-on elastically. The velocities of the ball A and B after collision will be respectively
A+0.5m/sand+0.3m/sB−0.3m/sand+0.5m/sC + 0.3 m//s and + 0.5 m//sD−0.5m/sand+0.3m/s
Two particles A and B are moving with constant velocities V1=ˆj and v2=2ˆi respectively in XY plane. At time t=0, the particle A is at co-ordinates (0,0) and B is at (-4,0). The angular velocities of B with respect to A at t=2s is (all physical quantities are in SI units)
View SolutionTwo particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
View SolutionVelocity and acceleration of a particle at time t=0are u=(2ˆi+3ˆj)m/sanda=(4ˆi+3ˆj)m/s2 respectively. Find the velocity and displacement if particle at t=2s.
View SolutionTwo particles A and B are situated at point (60,0) at t=0. The particle A move on a circle given by X2+Y2=3600 and with a speed 6πm/s, while B moves with a constant velocity.
Find the velocity of B so that the collision takes places between A and B at point (60,0).
View SolutionAt time t = 0, two bodies A and B at the same point. A moves with constant velocity υ and B starts from rest and moves with constant acceleration. Relative velocity of B w.r.t. A when the bodies meet each other is
View SolutionA charged particle of specific charge α moves with a velocity →v=v0ˆi in a magnetic field →B=B0√2(ˆj+ˆk). Then (specific charge=charge per unit mass)
View SolutionTwo particles A and B are located at point (0m,50m) at t=0. The particle A moves withy a constant velocity and the particle B moves on a circle of radius 50 m having centre at origin (0,0) as shown in figure. The pasrticle B has a constant speed 5πm/s. What will be the velocity of particle A so that both the pasrticles reach at point (50m,0m) simultaneously.
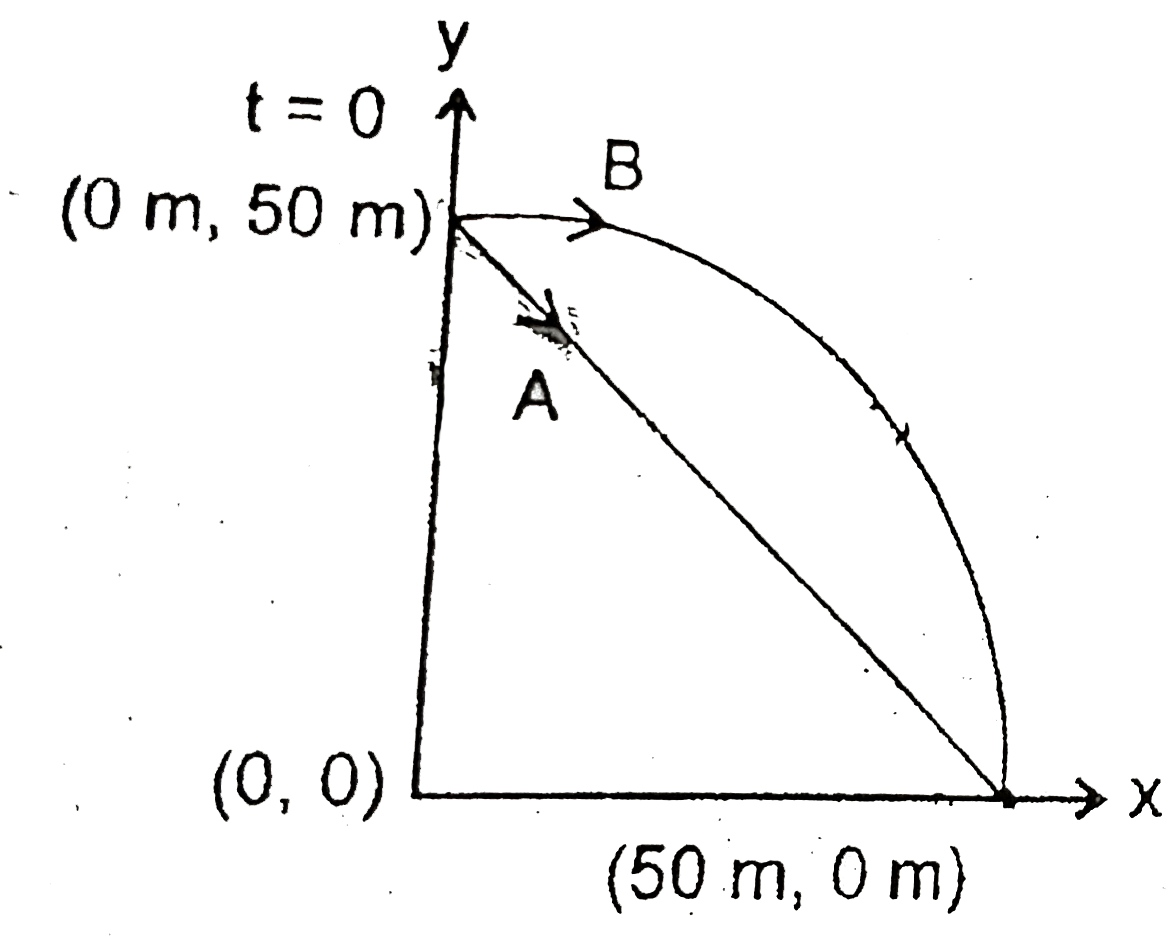
View Solution
