Two particles A and B are located in x−y plane at points (0,0) and (0,4m). They simultaneoulsy start moving with velocities vA=2ˆjm/s and vB=2ˆim/s. Select the correct alternative(s)
the distance between them is constant
The distance between them first decreases and then increases
the shortest distance between them is 2√2m
Time after which they are at minimum distances is 1s
The correct Answer is:B, C, D
Step by step video & image solution for Two particles A and B are located in x-y plane at points (0,0) and (0,4m). They simultaneoulsy start moving with velocities v_(A)=2hatjm//s and v_(B)=2hatim//s. Select the correct alternative(s) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN
10 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
Two particles A and B located at points (0,−10√3) and (0,0) in xy plane. They start moving simultaneously at time t=0 with constant velocities →VA=5ˆim/s and →VB=−5√3ˆjm/s, respectively. Time when they are closest to each other is found to be K/2 second. Find K. All distance are given in meter.
View SolutionAcceleration of a particle which is at rest at x=0 is →a=(4−2x)ˆi. Select the correct alternative (s).
View SolutionTwo particles A and B are projected simultaneously in the directins shown in figure with velocities vA=20m/sandvB=10m/s respectively. They collide in air after 12 s. Find
(a) the angle θ
(b) the distance x.
 .
.
View SolutionTwo particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then

View SolutionConsider
 .
.
The potential difference VA−VB is.
View SolutionTwo particles A and B are located at point (0m,50m) at t=0. The particle A moves withy a constant velocity and the particle B moves on a circle of radius 50 m having centre at origin (0,0) as shown in figure. The pasrticle B has a constant speed 5πm/s. What will be the velocity of particle A so that both the pasrticles reach at point (50m,0m) simultaneously.
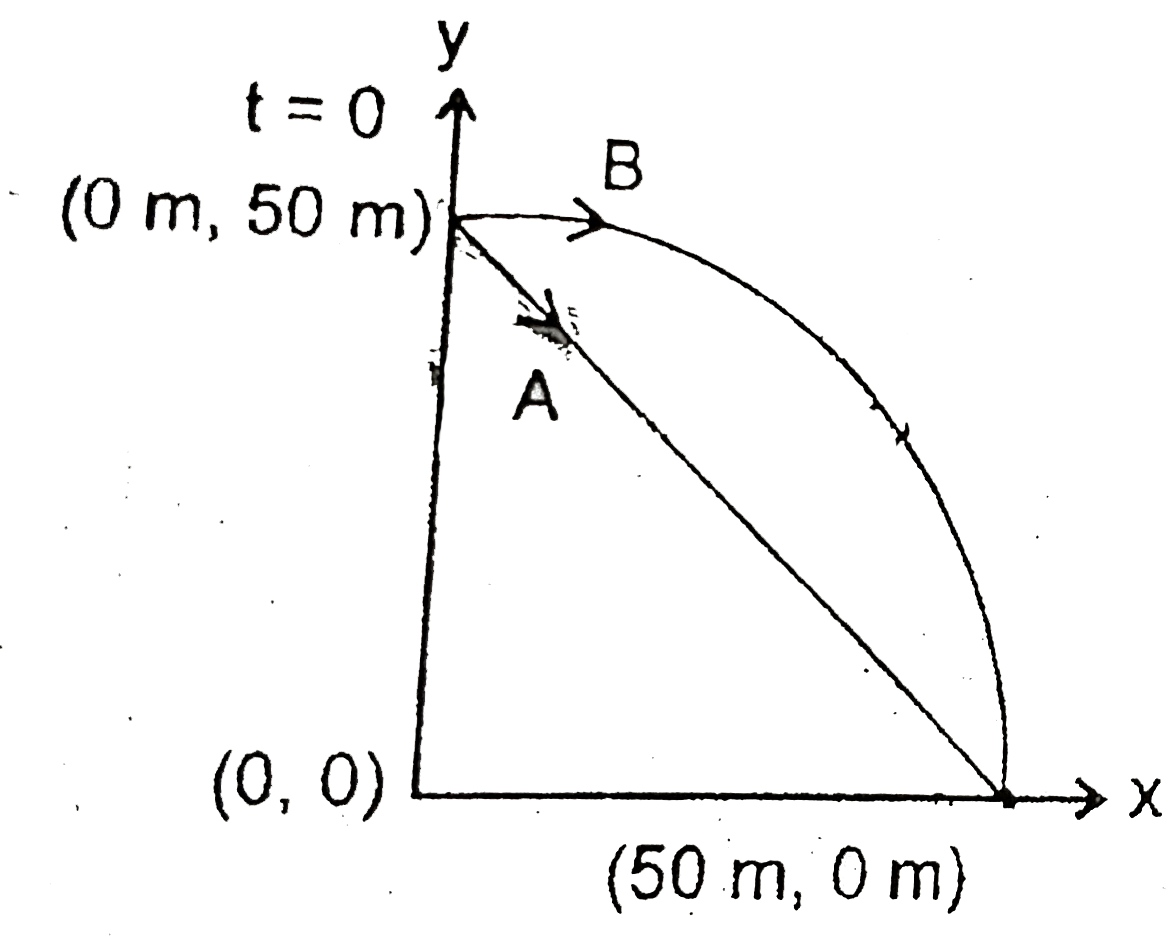
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

View SolutionTwo particles A and B are situated at point (60,0) at t=0. The particle A move on a circle given by X2+Y2=3600 and with a speed 6πm/s, while B moves with a constant velocity.
Find the velocity of B so that the collision takes places between A and B at point (60,0).
View SolutionA motorcyclist situated at origin is located at a distance 12m. Behind a car (Fig. 4.150).
 .
.
Att=0 the motorcyclist stars moving with a constant velocity v=8ms−1 and same time the car starts acceleration from rest with a=2ms&(−2), (a) When and wher do they meet?
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
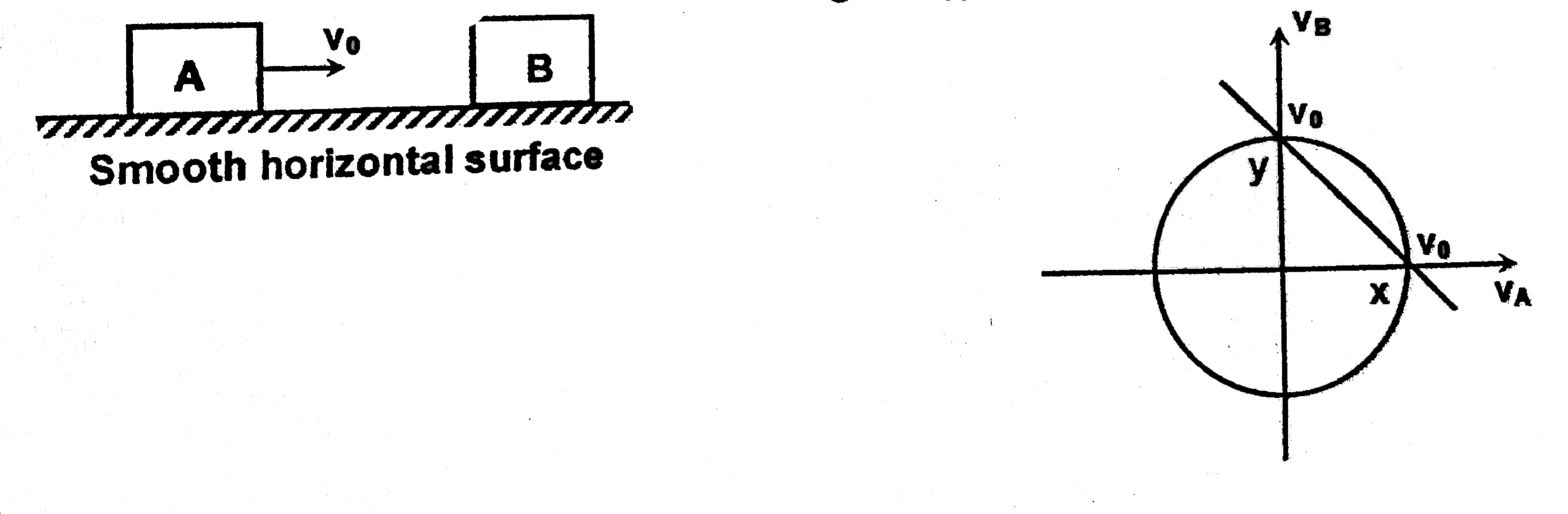
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is

View Solution
