On heating one end of a rod the temperature of the whole rod will be uniform when .
K = 1
K = 0
K = 100
K=∞
The correct Answer is:D
To solve the problem of when the temperature of a rod will become uniform upon heating one end, we can break down the explanation into clear steps:
1. Understanding Heat Transfer:
When one end of a rod is heated, heat begins to transfer from the hot end to the cooler end. The rate of heat transfer depends on the thermal conductivity of the material.
2. Thermal Conductivity (K):
The thermal conductivity (K) of a material is a measure of its ability to conduct heat. Higher values of K indicate that the material can transfer heat more efficiently.
3. Temperature Gradient:
The temperature gradient (dθ/dx) is the change in temperature (dθ) per unit length (dx) along the rod. If the temperature gradient is steep, it means there is a significant difference in temperature over a short distance, leading to a rapid heat transfer.
4. Condition for Uniform Temperature:
For the entire rod to reach a uniform temperature, the heat must be conducted through the rod without any significant temperature difference remaining. This means that the temperature gradient must approach zero (dθ/dx = 0).
5. Relation Between Heat Transfer and Thermal Conductivity:
The rate of heat transfer (Q) can be expressed as:
Q=K⋅A⋅dθdx
where A is the cross-sectional area. For the temperature to become uniform, we need to minimize the temperature gradient, which implies that the thermal conductivity (K) must be very high.
6. Conclusion:
If the thermal conductivity (K) approaches infinity, the heat transfer will occur instantaneously, leading to a uniform temperature throughout the rod. Thus, the condition for the temperature of the whole rod to be uniform is that the thermal conductivity must be infinite.
Final Answer:
The temperature of the whole rod will be uniform when the thermal conductivity (K) is infinite.
---
When one end of a rod is heated, heat begins to transfer from the hot end to the cooler end. The rate of heat transfer depends on the thermal conductivity of the material.
The thermal conductivity (K) of a material is a measure of its ability to conduct heat. Higher values of K indicate that the material can transfer heat more efficiently.
The temperature gradient (dθ/dx) is the change in temperature (dθ) per unit length (dx) along the rod. If the temperature gradient is steep, it means there is a significant difference in temperature over a short distance, leading to a rapid heat transfer.
For the entire rod to reach a uniform temperature, the heat must be conducted through the rod without any significant temperature difference remaining. This means that the temperature gradient must approach zero (dθ/dx = 0).
The rate of heat transfer (Q) can be expressed as:
Q=K⋅A⋅dθdx
where A is the cross-sectional area. For the temperature to become uniform, we need to minimize the temperature gradient, which implies that the thermal conductivity (K) must be very high.
If the thermal conductivity (K) approaches infinity, the heat transfer will occur instantaneously, leading to a uniform temperature throughout the rod. Thus, the condition for the temperature of the whole rod to be uniform is that the thermal conductivity must be infinite.
The temperature of the whole rod will be uniform when the thermal conductivity (K) is infinite.
Similar Questions
A thin rod of negligible mass and area of cross section S is suspended vertically from one end. Length of the rod is L0 at T∘C . A mass m is attached to the lower end of the rod so that when temperature of the rod is reduced to 0∘C its length remains L0 Y is the Young’s modulus of the rod and α is coefficient of linear expansion of rod. Value of m is :
View SolutionAssertion : Heat is supplied at constant rate from one end of a conducting rod. In steady state, temperature of all points of the rod becomes uniform.
Reason : In steady state, temperature of rod does not increase.
View Solution
Knowledge Check
Three metal rods of the same material and identical in all respect are joined as shown in the figure. The temperatures at the ends are maintained as indicated. Assuming no loss of heat from the curved surface of the rods, the temperature at the junction X would be
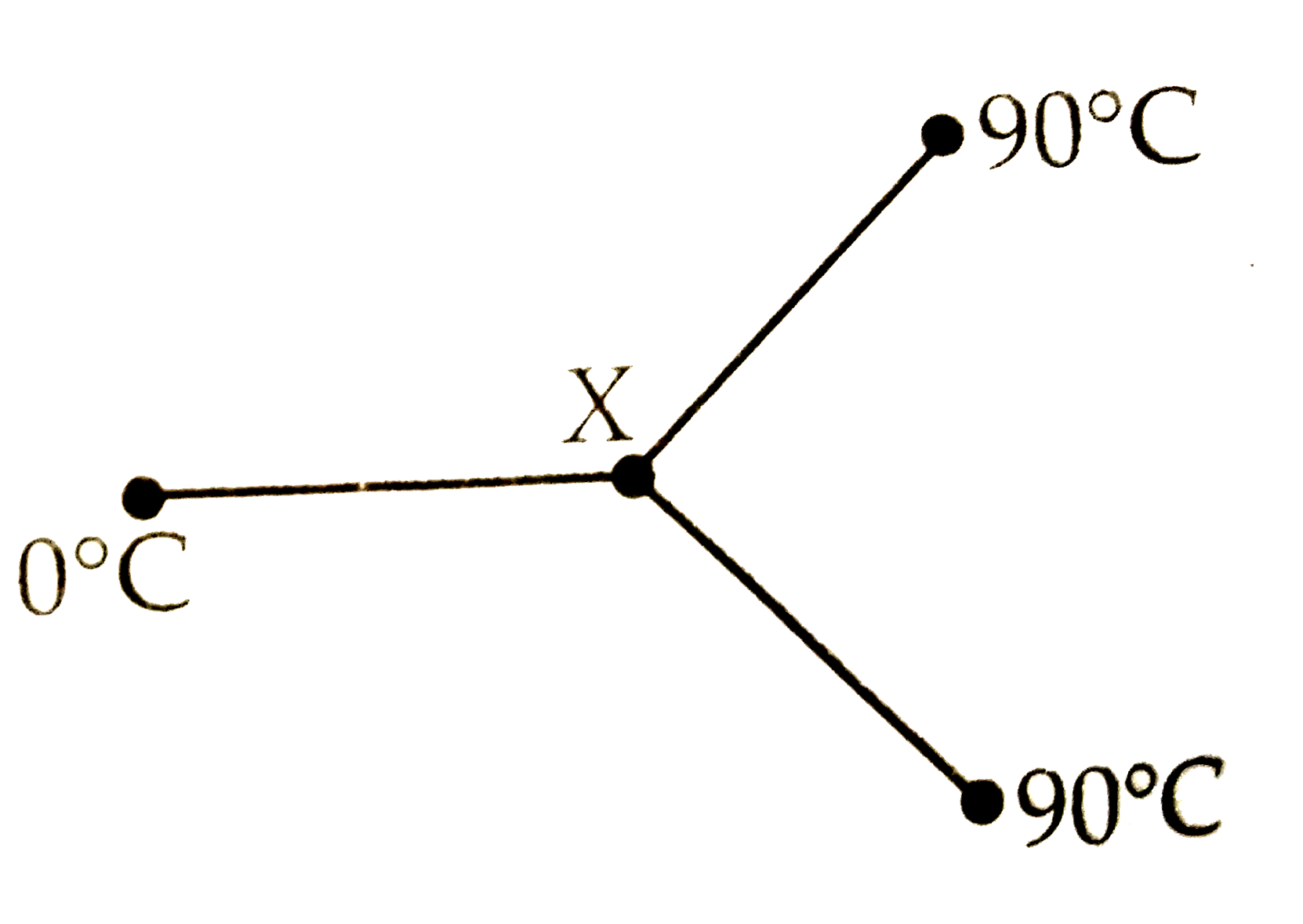 A45∘CB60∘CC30∘CD20∘C
A45∘CB60∘CC30∘CD20∘C
The temperature gradient in a rod of 0.5m length is 80∘C/m. It the temperature of hotter end of the rod is 30∘C, then the temperature of the cooler end is
View SolutionAssertion A metallic rod is fixed from two ends as shown in figure. When the temperature is increased compressive stresses are developed in the rod.

Reason At higher temperature, natural length of the rod will be more.
View SolutionA brass rod of length 1m is fixed to a vertical wall at one end, with the other end keeping free to expand. When the temperature of the rod is increased by 120∘C, the length increases by 3cm. What is the strain?
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View SolutionA uniform rod is placed vertically on a smooth surface and then released . Then,
View SolutionA slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
View SolutionTwo similar rods are joined as shown in figure. Then temperature of junction is (assume no heat loss through lateral surface of rod and temperatures at the ends are shown in steady state )
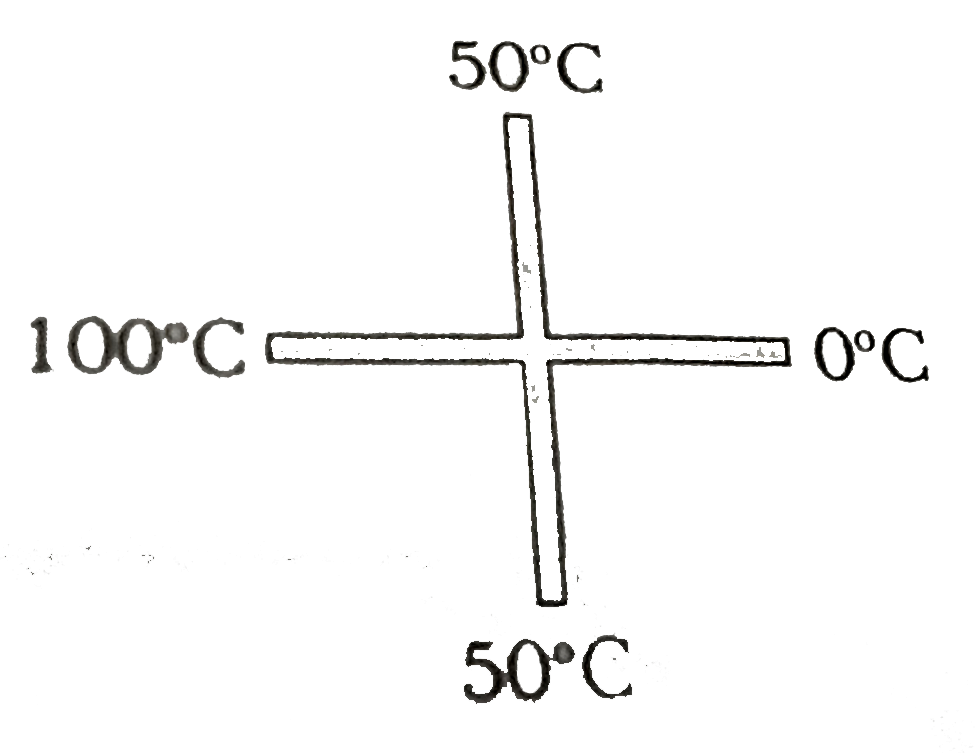
View Solution
