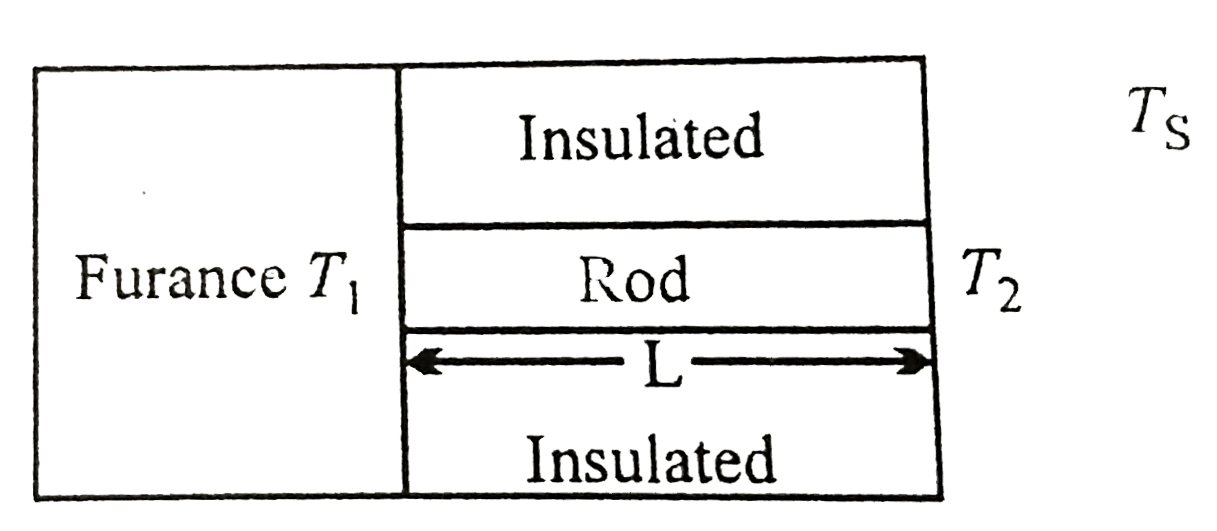
One end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

Rate of heat conduction through rod=rate of the heat lost from right end of the rod.
KA(T1−T2)L=eAσ(T42−T4s) (i)
Given that T1=Ts+ΔT
T42=(Ts+ΔT)4=T45(1+ΔTTs)
Using binomial expansion, we have
T42=T4s(1+4ΔTTs) (as ΔT<<Ts)
T42=−T4s=4(ΔT)(T3s)
Subsituting in Eq. (i), we have
K(T1−TS−ΔT)L=4eσT3sΔT
K(T1−Ts)L=(4eσT3s+KL)ΔT
ΔT=K(T1−Ts)(4eσLT3s+K)
Comparing with the given relation, proportionality constant
=K4eσLT3s+K
Topper's Solved these Questions
Similar Questions
One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionA solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
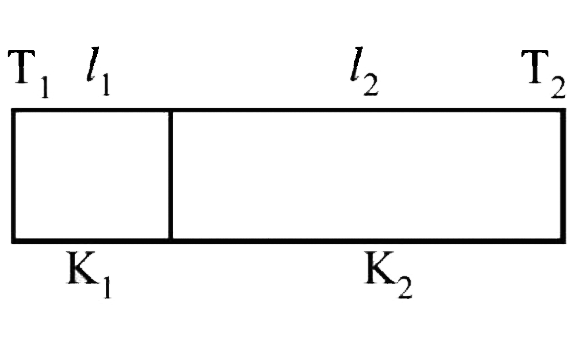
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionIf K1= Rate constant at temperature T1 and k2 rate constant at temperature T2 for a first order reaction, then which of the following relation is correct ?
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View Solution