In an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
Q2
Q√3
Q√2
Q
The correct Answer is:C
To solve the problem, we need to find the charge on the capacitor when the energy is equally distributed between the electric field (in the capacitor) and the magnetic field (in the inductor) in an oscillating LC circuit.
1. Understanding the Energy in LC Circuit:
- The total energy E in an LC circuit is conserved and can be expressed as the sum of the energy stored in the capacitor and the energy stored in the inductor:
E=UC+UL
- The energy stored in the capacitor UC is given by:
UC=12CV2=12Q2C
- The energy stored in the inductor UL is given by:
UL=12LI2
2. Condition for Equal Energy Distribution:
- When the energy is equally distributed, we have:
UC=UL
- Therefore, we can write:
12Q2C=12LI2
3. Relating Charge and Current:
- The current I in the circuit can be expressed in terms of charge q on the capacitor:
I=−dqdt
- At the point where the energy is equally distributed, we can denote the charge on the capacitor as q.
4. Substituting the Charge:
- At the point of equal energy distribution, we can express the energy in terms of charge q:
UC=12q2C
UL=12L(−dqdt)2
- Since UC=UL, we can equate:
12q2C=12L(−dqdt)2
5. Finding the Charge q:
- Given that the maximum charge on the capacitor is Q, we can find the charge when the energy is equally distributed:
q=Q√2
Final Answer:
The charge on the capacitor when the energy is stored equally between the electric and magnetic fields is:
q=Q√2
- The total energy E in an LC circuit is conserved and can be expressed as the sum of the energy stored in the capacitor and the energy stored in the inductor:
E=UC+UL
- The energy stored in the capacitor UC is given by:
UC=12CV2=12Q2C
- The energy stored in the inductor UL is given by:
UL=12LI2
- When the energy is equally distributed, we have:
UC=UL
- Therefore, we can write:
12Q2C=12LI2
- The current I in the circuit can be expressed in terms of charge q on the capacitor:
I=−dqdt
- At the point where the energy is equally distributed, we can denote the charge on the capacitor as q.
- At the point of equal energy distribution, we can express the energy in terms of charge q:
UC=12q2C
UL=12L(−dqdt)2
- Since UC=UL, we can equate:
12q2C=12L(−dqdt)2
- Given that the maximum charge on the capacitor is Q, we can find the charge when the energy is equally distributed:
q=Q√2
The charge on the capacitor when the energy is stored equally between the electric and magnetic fields is:
q=Q√2
Similar Questions
Knowledge Check
A fully charged capacitor C with initial charge q0 is connected to a coil of self inductance L at t=0. The time at which the energy is stored equally between the electric and the magnetic fields is
Aπ4√LCB2π√LCC√LCDπ√LC
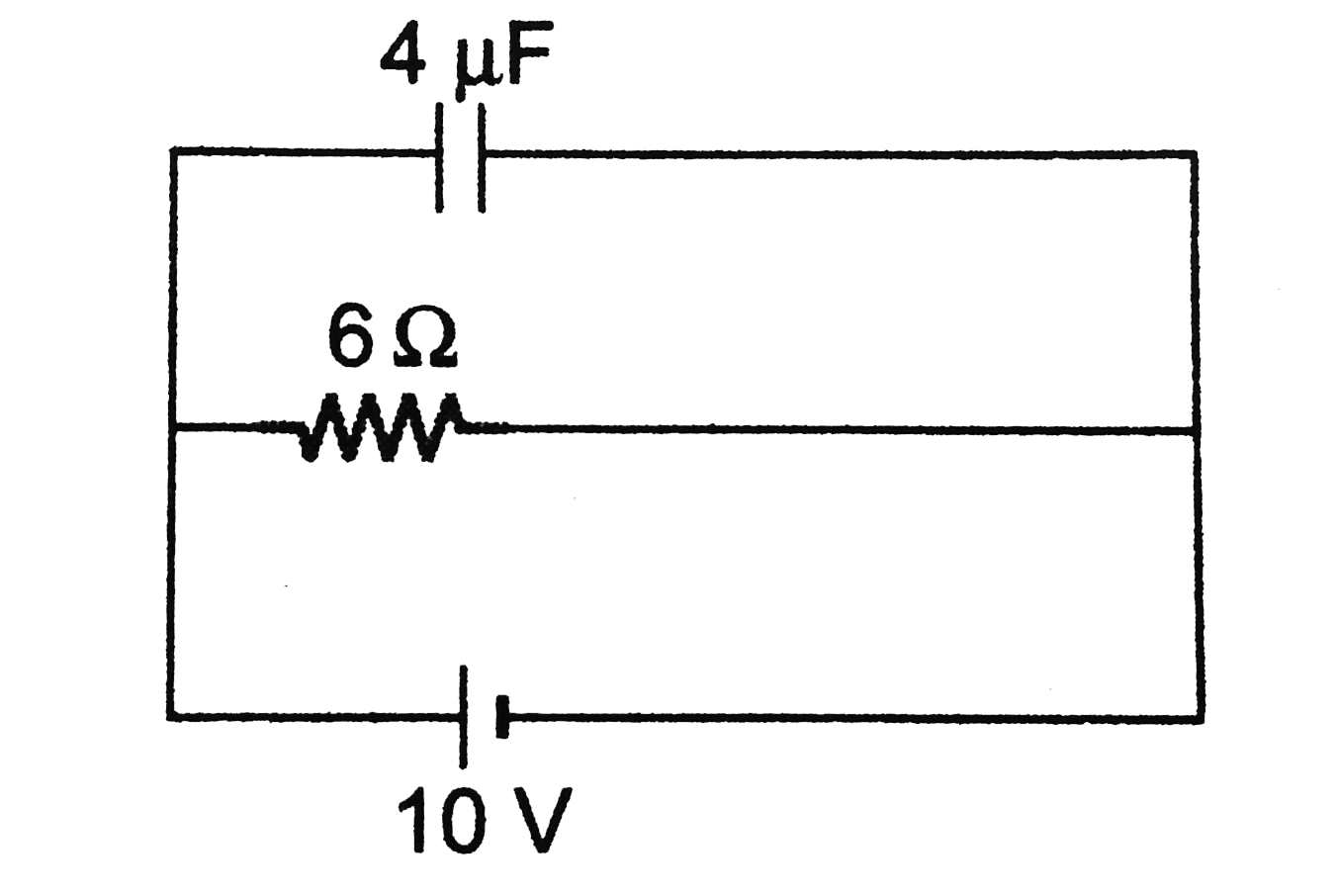
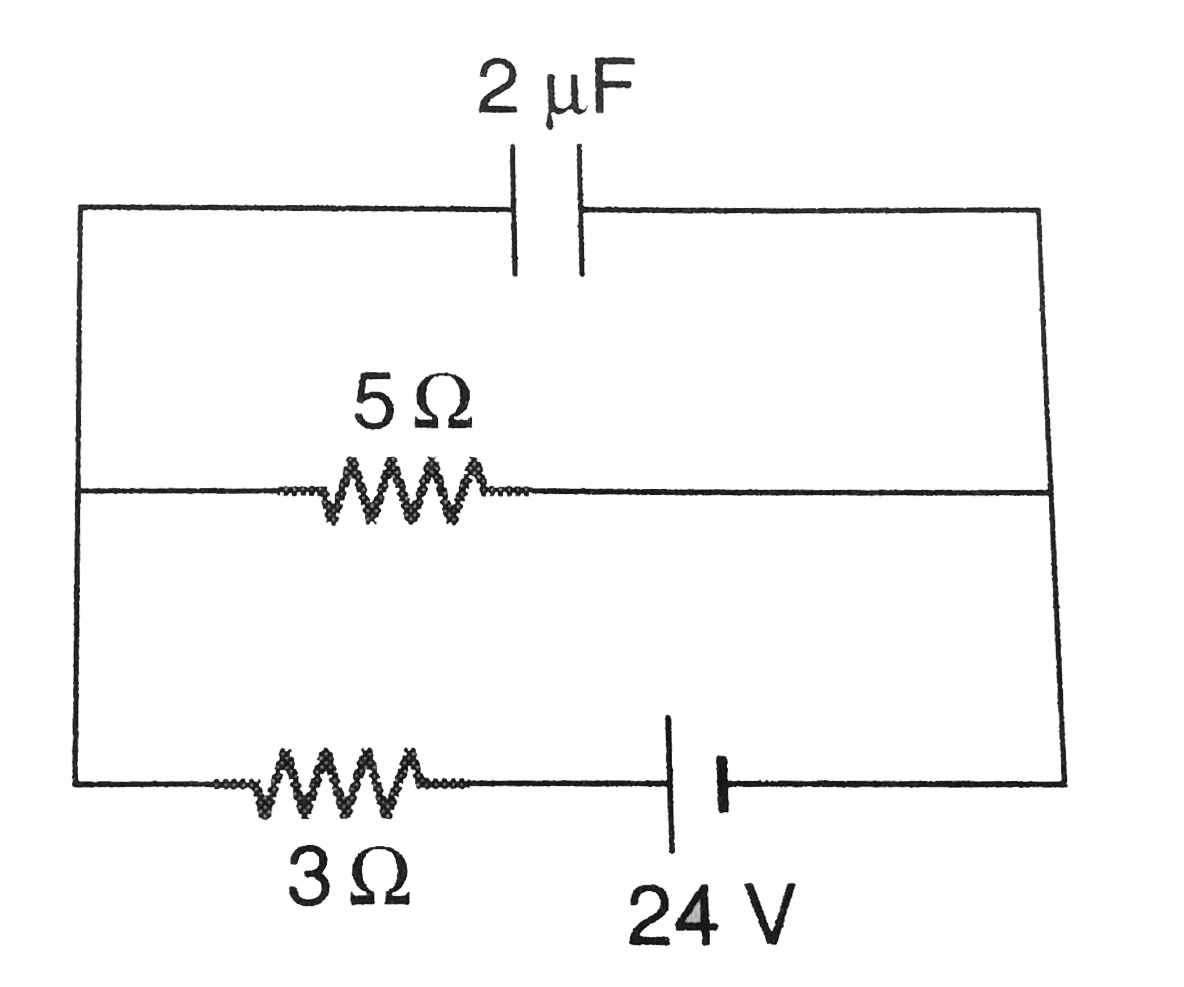
Find the charge stored in the capacitor.
View SolutionIn LC circuit the maximum charge in capacitor is q0. Then maximum value of rate of change of current is
View SolutionDisplacement current is maximum during charging of capacitor. When charge on the capacitor is
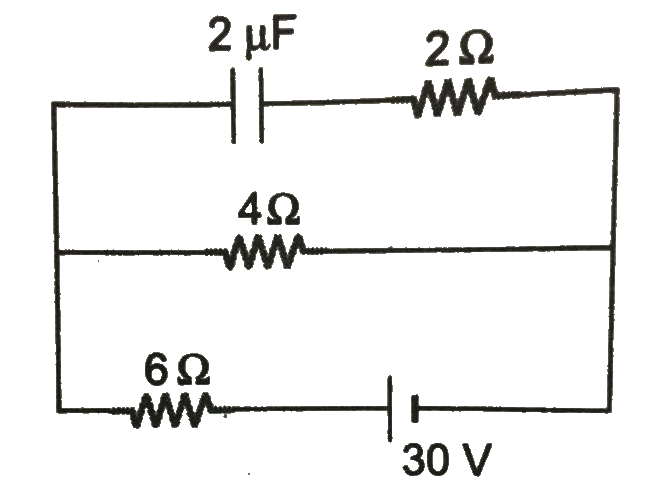
View SolutionFind the charged stored in all the capacitors
View SolutionIn a charged capacitor, the energy resides in
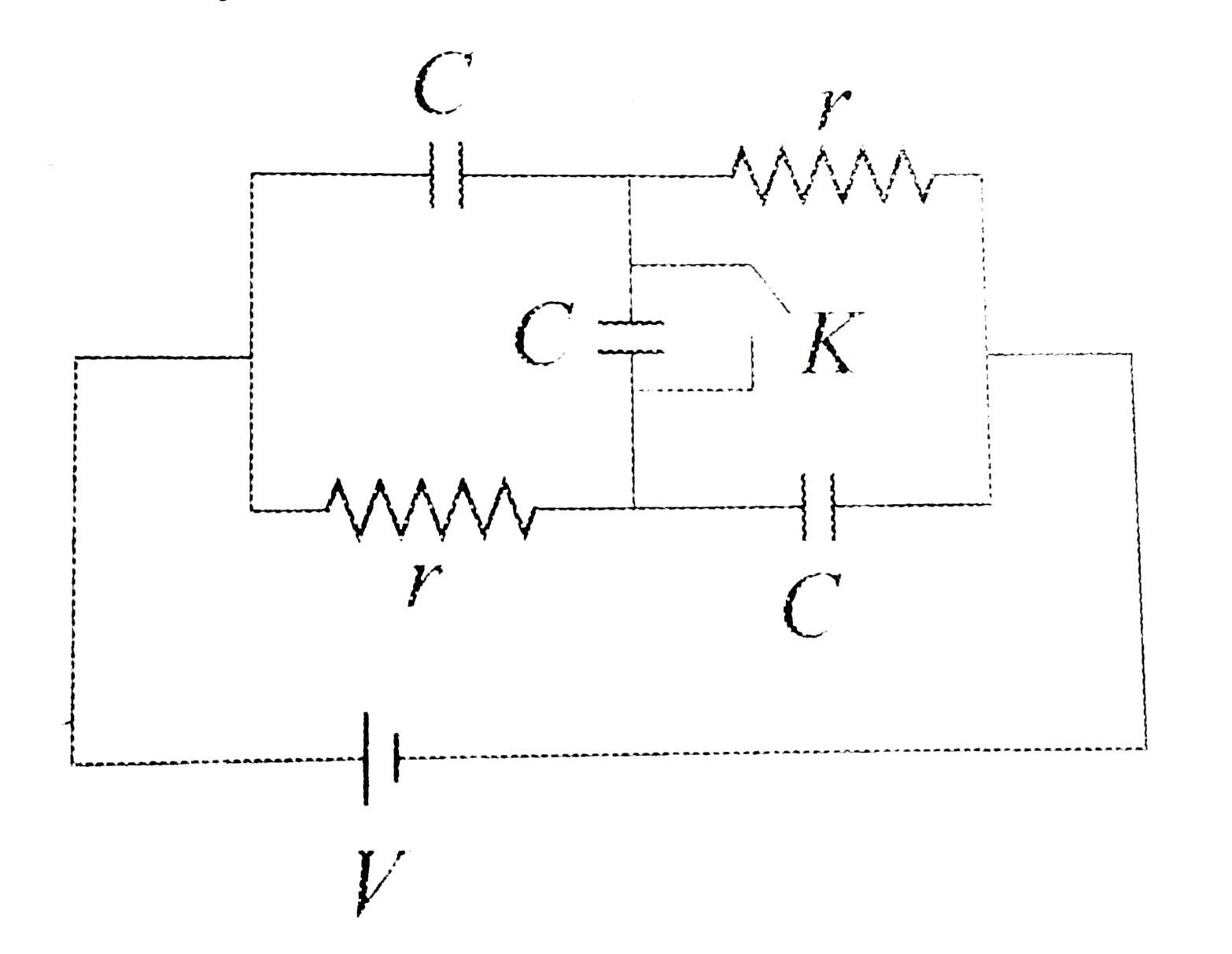
View SolutionIn the circuit what is the change of total electrical energy stored in the capacitors when the key is pressed ?
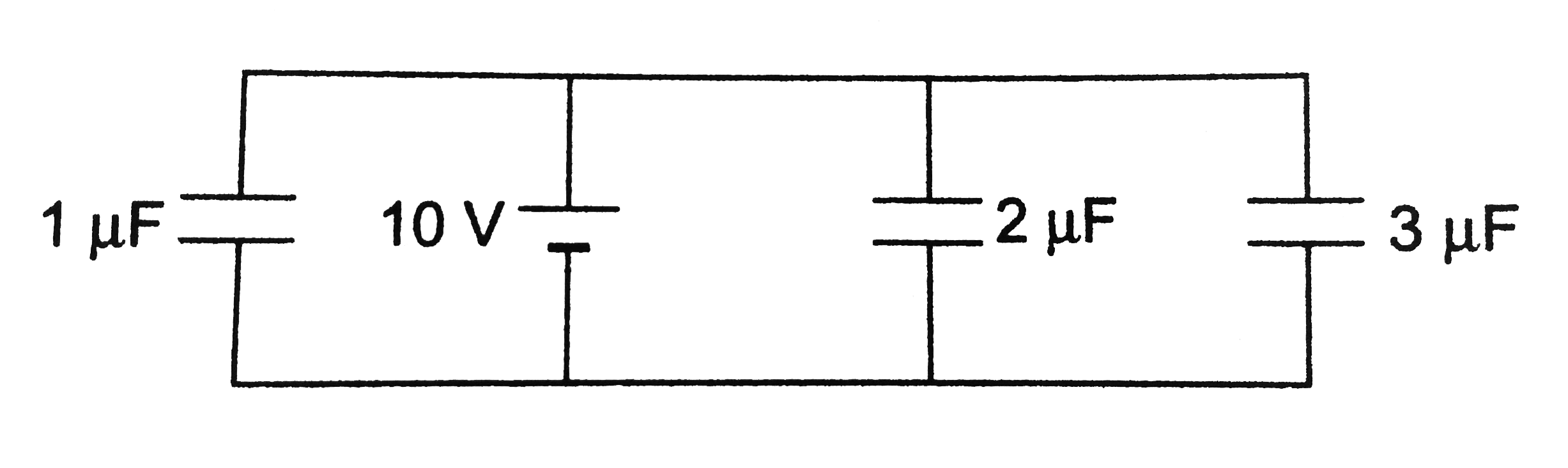
View SolutionDetermine to charge on the capacitor in the following circuit :
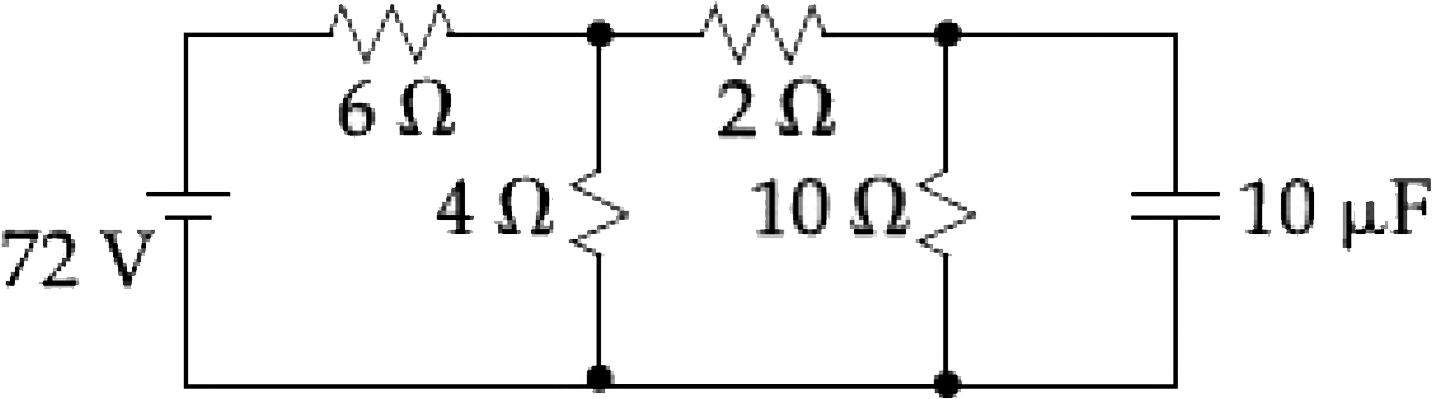
View Solution