In LC circuit the maximum charge in capacitor is q0. Then maximum value of rate of change of current is
q0L−12C−12
q0L−1C−1
q0LC
q0L−1C
To solve the problem, we need to find the maximum value of the rate of change of current in an LC circuit, given that the maximum charge in the capacitor is q0.
1. Understanding the LC Circuit:
- An LC circuit consists of an inductor (L) and a capacitor (C) and exhibits oscillatory behavior where energy oscillates between the capacitor and the inductor.
2. Charge in the Capacitor:
- The charge q(t) on the capacitor as a function of time can be expressed as:
q(t)=q0cos(ωt)
- Here, q0 is the maximum charge, and ω is the angular frequency of the oscillation.
3. Finding the Current:
- The current I(t) in the circuit is defined as the rate of change of charge:
I(t)=dqdt
- Differentiating q(t):
I(t)=ddt(q0cos(ωt))=−q0ωsin(ωt)
4. Finding the Rate of Change of Current:
- Now, we need to find the rate of change of current, which is:
dIdt=ddt(−q0ωsin(ωt))
- Differentiating again:
dIdt=−q0ω2cos(ωt)
5. Maximum Value of Rate of Change of Current:
- The maximum value of dIdt occurs when cos(ωt)=1:
(dIdt)max=q0ω2
6. Expressing ω:
- The angular frequency ω for an LC circuit is given by:
ω=1√LC
- Therefore, substituting this into our equation:
(dIdt)max=q0(1√LC)2=q0LC
Final Answer:
The maximum value of the rate of change of current in the LC circuit is:
q0LC
- An LC circuit consists of an inductor (L) and a capacitor (C) and exhibits oscillatory behavior where energy oscillates between the capacitor and the inductor.
- The charge q(t) on the capacitor as a function of time can be expressed as:
q(t)=q0cos(ωt)
- Here, q0 is the maximum charge, and ω is the angular frequency of the oscillation.
- The current I(t) in the circuit is defined as the rate of change of charge:
I(t)=dqdt
- Differentiating q(t):
I(t)=ddt(q0cos(ωt))=−q0ωsin(ωt)
- Now, we need to find the rate of change of current, which is:
dIdt=ddt(−q0ωsin(ωt))
- Differentiating again:
dIdt=−q0ω2cos(ωt)
- The maximum value of dIdt occurs when cos(ωt)=1:
(dIdt)max=q0ω2
- The angular frequency ω for an LC circuit is given by:
ω=1√LC
- Therefore, substituting this into our equation:
(dIdt)max=q0(1√LC)2=q0LC
The maximum value of the rate of change of current in the LC circuit is:
q0LC
Similar Questions
In an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View Solution
Knowledge Check
The maximum value of photoelectric current is called
Abase currentBsaturation currentCcollector currentDemitter current
Assertion : Angular frequency of LC oscillations is 2rad/s and maximum current in the circuit is 1A. Then, maximum rate of change of current should be 2A/s.
Reason: (dIdt)max=(Imax)ω
View SolutionIn an LC circuit the capacitor has maximum charge q0. The value of (dIdt)max is

View SolutionAn L-C circuit contains a 0.60 H inductor and a 25μF capacitor. What is rate of change of current when the charges on the capacitor is3.0×10−5C?
View SolutionAn L−C circuit consists of an inductor coil withh L=50.0mH and 20.0μF capacitor. There is negligible resistance in the circuit. The circuit is driven by a voltage source with V=V0cosωt. If V0=5.00mV and the frequency is twice the resonance frequency, determine.
a. the maximum charge on the capacitor.
b. the maximum current in the circuit.
c. the phase relationship between the voltages across the inductor, the capacitor and the sourse.
View SolutionAssertion In the figure, just after closing the switch the potential drop across inductor is maximum.
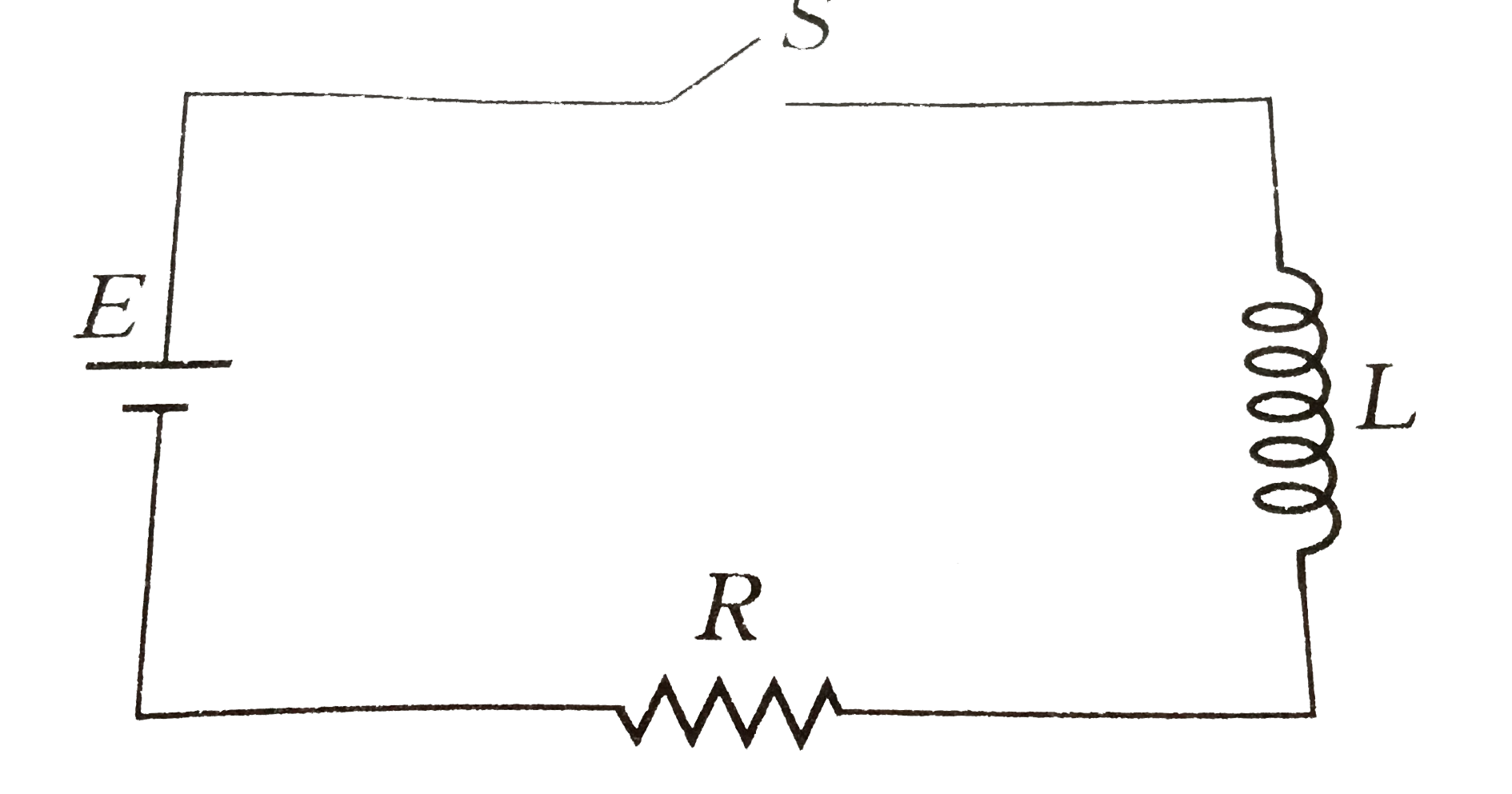
Reason The rate of change of current just after closing the switch is maximum.
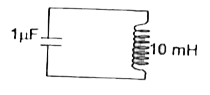
View SolutionIn the given circuit, if initial charge on the capacitor is 100μC, then the maximum current is (Initially, the inductor is fully deenergized)
View SolutionAn oscillator circuit contains an inductor 0.05 H and a capacitor of capacity 80μF. When the maximum voltage across the capacitor is 200 V, the maximum current (in amperes) in the circuit is
View Solution
