For the potential energy function shown in fig. there will be an unstable equilibrium at position

A
B
C
None of the above
The correct Answer is:B
Step by step video & image solution for For the potential energy function shown in fig. there will be an unstable equilibrium at position by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium is
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity is
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium distance is given by
View SolutionSTATEMENT-1: If potential energy of a dipole in stable equilibrium position is zero, its potential energy is unstable equilibrium position will be 2pE, where p and E represent the dipole moment and electric field respectively
and
STATEMENT-2 : The potential energy of a dipole is minimum in stable equilibruim position and maximum in unstable equilibrium position.
View SolutionFor the potential energy curve shown shown in figure.
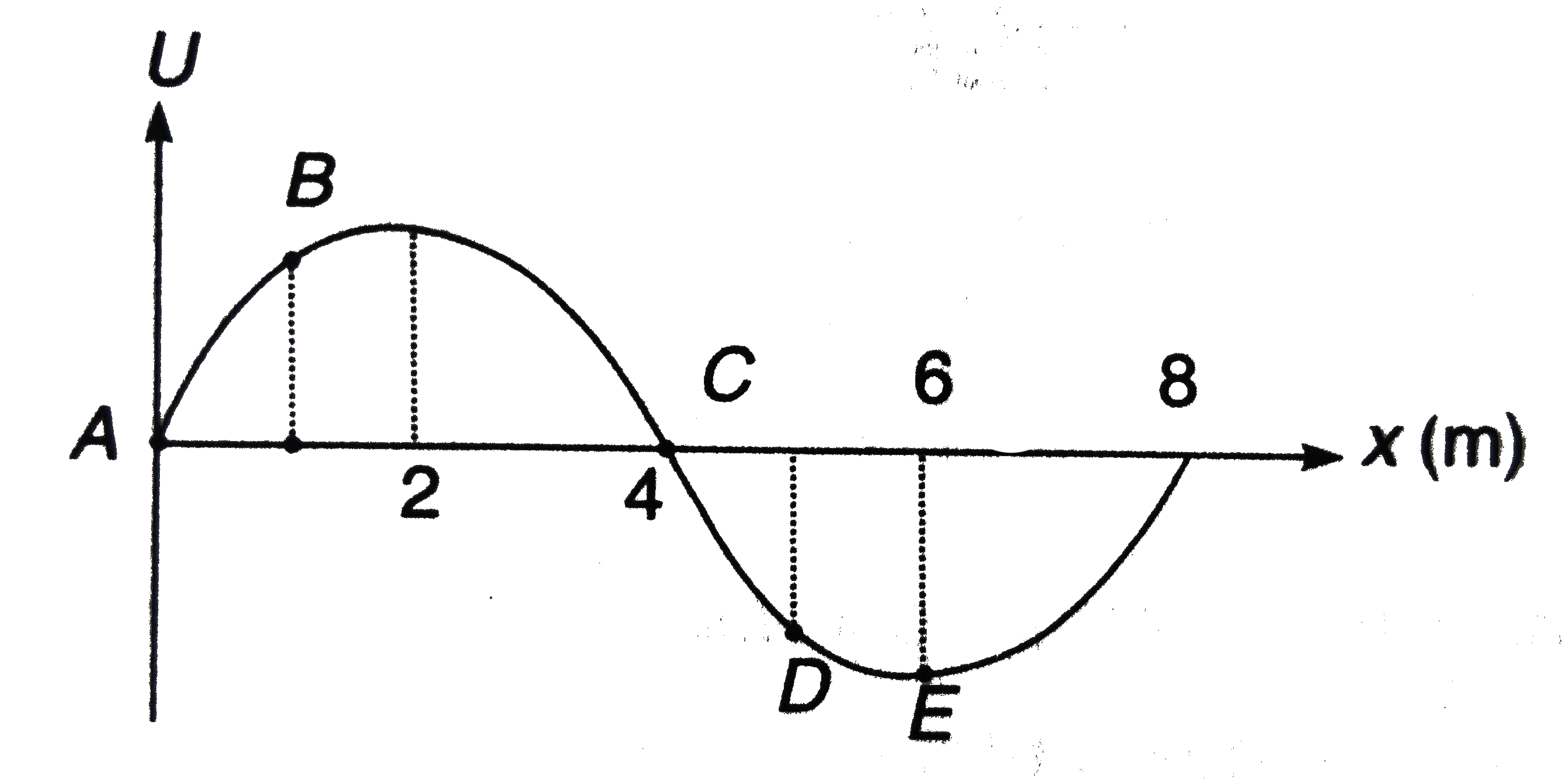
(a) Find directions of force at points A,B,C,D and E.
(b) Find positions of stable, unstable and neutral equilibriums.
View SolutionFor the potential energy curve shown in figure.
(a) Determine whether the force Fx is positive, negative, or zero at the five points indicated, (b) Indicate points of stable, unstable, and neutral equilibrium, (c) Sketch the curve for Fx versus x from x=0 to x=8m.

View SolutionFind the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

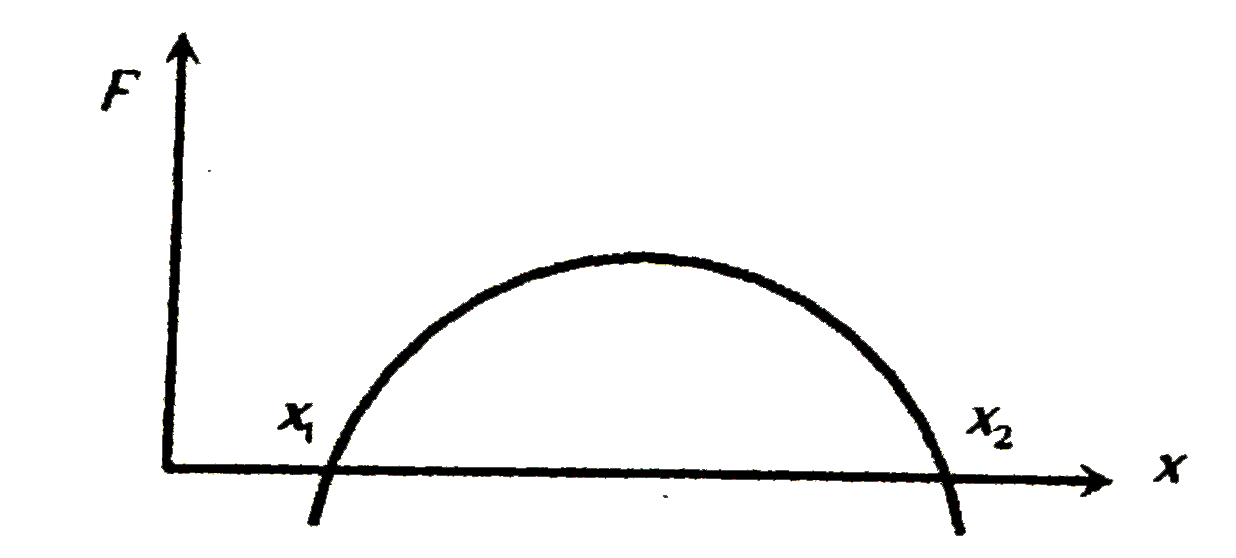
View SolutionThe force acting on a body moving along x -axis varies with the position of the particle as shown in the fig. The body is in stable equilibrium at.
View SolutionThe potential energy of a harmonic oscillator of mass 2kg in its equilibrium position is 5 joules. Its total energy is 9 joules and its amplitude is 1cm. Its time period will be
View SolutionThe work done in rotating a bar magnet of magnetic moment M from its unstable equilibrium position to its stable equilibrium position in a uniform magnetic field B is
View Solution