Electromagnetic radiations of wavelength 2000Å are incident on a metal surface which has a work function 5.01eV The stopping potential for the given setup is
1.19 eV
6.19 eV
3.19 eV
4.19 eV
The correct Answer is:A
To find the stopping potential for the given setup, we can use the photoelectric equation:
E=eV0=hcλ−Φ
Where:
- E is the energy of the incident photons,
- e is the charge of an electron,
- V0 is the stopping potential,
- h is Planck's constant (6.626×10−34Js),
- c is the speed of light (3×108m/s),
- λ is the wavelength of the incident radiation,
- Φ is the work function of the metal.
Given:
- Wavelength \lambda = 2000 \, \text{Å} = 2000 \times 10^{-10} \, \text{m} = 2 \times 10^{-7} \, \text{m}
- Work function Φ=5.01eV
Step 1: Calculate the energy of the incident photons E
Using the formula for energy:
E=hcλ
Substituting the values:
E=(6.626×10−34Js)(3×108m/s)2×10−7m
Step 2: Calculate E
Calculating the numerator:
E=(6.626×10−34)(3×108)2×10−7
E=1.9878×10−252×10−7
E=9.939×10−19J
Step 3: Convert energy from Joules to electron volts
To convert Joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
E=9.939×10−19J1.6×10−19J/eV
E≈6.21eV
Step 4: Use the photoelectric equation to find the stopping potential V0
Now substituting back into the photoelectric equation:
eV0=E−Φ
V0=E−Φe
Substituting the values:
V0=6.21eV−5.01eV
V0=1.20eV
Step 5: Conclusion
Thus, the stopping potential V0 is approximately 1.20V.
Final Answer:
The stopping potential for the given setup is approximately 1.20V.
---
- E is the energy of the incident photons,
- e is the charge of an electron,
- V0 is the stopping potential,
- h is Planck's constant (6.626×10−34Js),
- c is the speed of light (3×108m/s),
- λ is the wavelength of the incident radiation,
- Φ is the work function of the metal.
- Wavelength \lambda = 2000 \, \text{Å} = 2000 \times 10^{-10} \, \text{m} = 2 \times 10^{-7} \, \text{m}
- Work function Φ=5.01eV
The stopping potential for the given setup is approximately 1.20V.
Similar Questions
Light of wavelength 2000 Å falls on a metallic surface whose work function is 4.21 eV. Calculate the stopping potential
View SolutionElectromagnetic radiation of wavelength 3000Å is incident on an isolated platinum surface of work- function 6.30 eV. Due to the radiation, the
View SolutionMonochromatic light of wavelength 198 nm is incident on the surface of a metal, whose work function is 2.5 eV. Calculate the stopping potential.
View SolutionLight of energy 2.0 eV falls on a metal of work function 1.4 eV . The stopping potential is
View SolutionLight of wavelength 3000Å is incident on a metal surface whose work function is 1 eV. The maximum velocity of emitted photoelectron will be
View SolutionLight of wavelenght 5000Å fall on a metal surface of work function 1.9eV Find
a. The energy of photon
View SolutionLight of wavelength 2000Å is incident on a metal surface of work function 3.0 eV. Find the minimum and maximum kinetic energy of the photoelectrons.
View SolutionRadiation from a hydrogen discharge tube ( energy of photons ≤13.6eV) goes through a fliter which transmits only waves of wavelength greater than 4400Å and is incident on a metal of work function 2.0eV. If stopping potential is n×10−2 volts. Find the value of 'n'
View Solution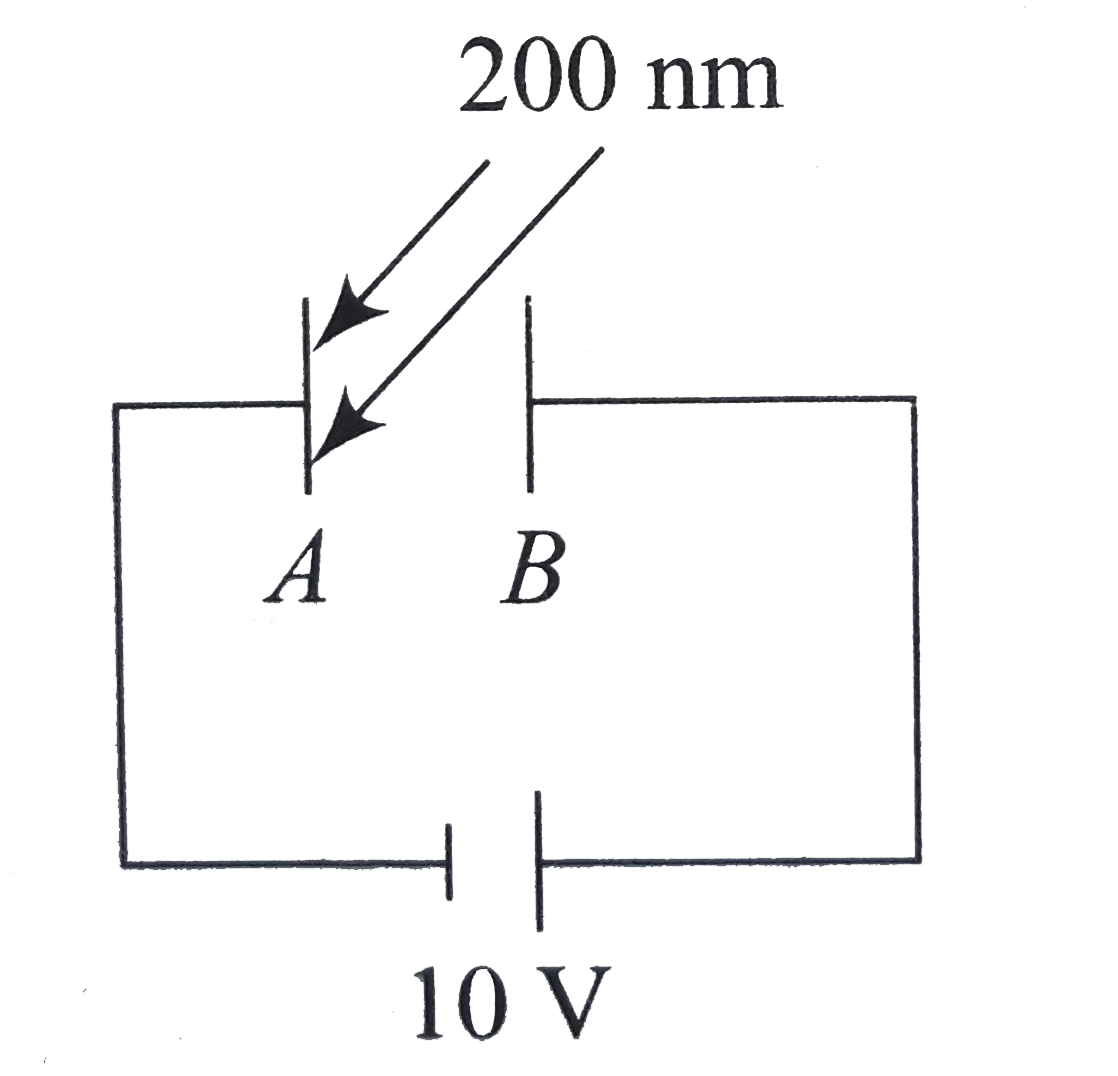
In Fig. electromagnetic radiations of wavelength 200nm are incident on a metallic plate A. the photoelectrons are accelerated by a potential difference of 10 V. These electrons strike another metal plate B from which electromagnetic radiations are emitted. The minimum wavelength of emitted photons is 100nm. If the work function of metal A is found to be (×x10−1)ev, then find the value of x. (Given hc=1240eV nm)
View SolutionLight of wavelength 500nm is incident on a metal with work function 2.28eV. The de Broglie wavelength of the emitted electron is
View Solution