If the magnetic field is parallel to a surface then, the magnetic flux through the surface is
(a)zero
(b)small but not zero
(c)infinite
(d)large but not infinite
The correct Answer is:A
To solve the problem of determining the magnetic flux through a surface when the magnetic field is parallel to that surface, we can follow these steps:
1. Understanding Magnetic Flux:
- Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which it passes, multiplied by the cosine of the angle (θ) between the magnetic field and the normal (perpendicular) to the surface.
- The formula for magnetic flux is given by:
Φ=B⋅A⋅cos(θ)
2. Identifying the Angle:
- In this scenario, we are told that the magnetic field is parallel to the surface. This means that the angle (θ) between the magnetic field and the area vector (which is perpendicular to the surface) is 90 degrees.
3. Calculating Cosine of the Angle:
- We know that:
cos(90∘)=0
4. Substituting Values into the Flux Formula:
- Now, substituting the values into the magnetic flux formula:
Φ=B⋅A⋅cos(90∘)=B⋅A⋅0
5. Conclusion:
- Therefore, the magnetic flux through the surface is:
Φ=0
Final Answer:
The magnetic flux through the surface is 0.
- Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which it passes, multiplied by the cosine of the angle (θ) between the magnetic field and the normal (perpendicular) to the surface.
- The formula for magnetic flux is given by:
Φ=B⋅A⋅cos(θ)
- In this scenario, we are told that the magnetic field is parallel to the surface. This means that the angle (θ) between the magnetic field and the area vector (which is perpendicular to the surface) is 90 degrees.
- We know that:
cos(90∘)=0
- Now, substituting the values into the magnetic flux formula:
Φ=B⋅A⋅cos(90∘)=B⋅A⋅0
- Therefore, the magnetic flux through the surface is:
Φ=0
The magnetic flux through the surface is 0.
Similar Questions
The electric flux through the surface

View SolutionThe electric flux through the surface

View SolutionThe electric flux through the surface

View SolutionA surface enclosed an electric dipole, the flux through the surface is -
View SolutionAssertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity ω as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field.
Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.
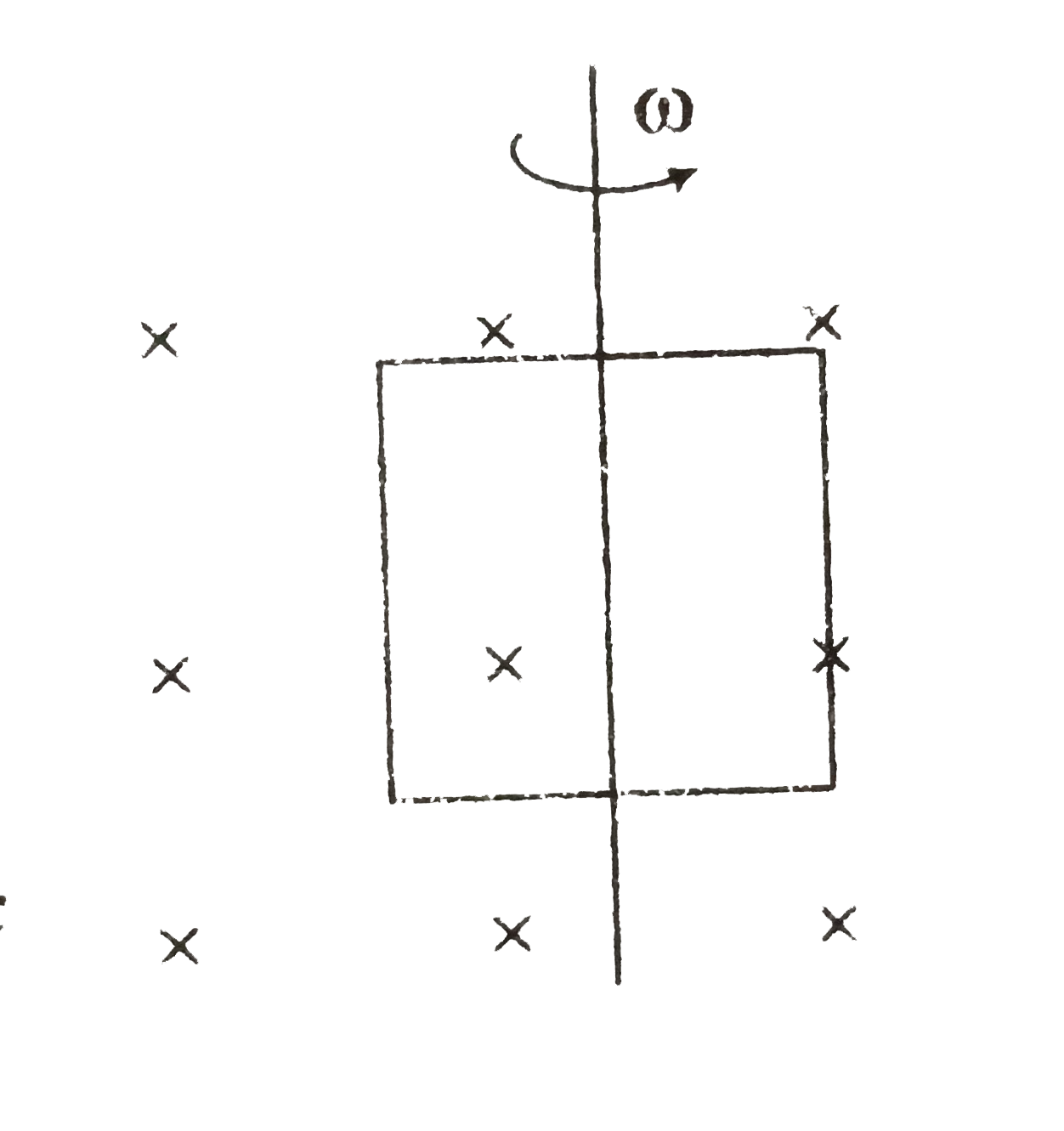
View SolutionWhen a 10 μC charge is enclosed by a closed surface, the flux passing through the surface is ϕ. Now another 10 µC charge is placed inside the closed surface, then the flux passing through the surface is ______.
View SolutionIf the flux of the electric field through a closed surface is zero,
View SolutionConsider a short bar magnet forming a magnetic dipole enclosed by an imaginary co-axial cylindrical surface with circular base area. Magnet is at the middle of cylinder. If magnetic flux through one of the circular base is ϕ0 then the magnetic flux through the other circular base will be:
View SolutionConsider a short bar magnet forming a magnetic dipole enclosed by an imaginary co-axial cylindrical surface with circular base area. Magnet is at the middle of cylinder. If magnetic flux through one of the circular base is phi _(0) then the magnetic flux through the other circular base will be:
View SolutionA surface encloses an electric dipole. The electric flux through the surface is
View Solution
