A particle is projected in the X−Y plane. 2sec after projection the velocity of the particle makes an angle 45∘ with the X−axis. 4sec after projection, it moves horizontally. Find the velocity of projection (use g=10ms−2).
20√5ms−1
10√5ms−1
5√5ms−1
2√5ms−1
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the particle projected in the X-Y plane.
Step 1: Understanding the Motion
The particle is projected at an angle with respect to the horizontal (X-axis). We know that:
- After 2 seconds, the velocity makes an angle of 45° with the X-axis.
- After 4 seconds, the particle moves horizontally, meaning its vertical velocity component is zero at that time.
Step 2: Analyzing the Vertical Motion
At the highest point of the trajectory (4 seconds after projection), the vertical component of the velocity (Vy) is zero. We can use the equation of motion for vertical velocity:
Vy=Uy−gt
At t=4 seconds:
0=Uy−g⋅4
Given g=10m/s2:
0=Uy−40
Thus, we find:
Uy=40m/s
Step 3: Analyzing the Motion at 2 Seconds
At t=2 seconds, the velocity makes an angle of 45° with the X-axis. This means:
Vx=Vy
Using the vertical motion equation again at t=2 seconds:
Vy=Uy−g⋅2
Substituting Uy=40:
Vy=40−20=20m/s
Since Vx=Vy:
Vx=20m/s
Step 4: Finding the Initial Velocity Components
Now we have:
- Uy=40m/s
- Ux=Vx=20m/s
Step 5: Calculating the Magnitude of the Initial Velocity
The magnitude of the initial velocity U can be calculated using the Pythagorean theorem:
U=√U2x+U2y
Substituting the values:
U=√(20)2+(40)2
U=√400+1600
U=√2000
U=20√5m/s
Final Answer
The velocity of projection is:
U=20√5m/s
The particle is projected at an angle with respect to the horizontal (X-axis). We know that:
- After 2 seconds, the velocity makes an angle of 45° with the X-axis.
- After 4 seconds, the particle moves horizontally, meaning its vertical velocity component is zero at that time.
At the highest point of the trajectory (4 seconds after projection), the vertical component of the velocity (Vy) is zero. We can use the equation of motion for vertical velocity:
Vy=Uy−gt
At t=4 seconds:
0=Uy−g⋅4
Given g=10m/s2:
0=Uy−40
Thus, we find:
Uy=40m/s
At t=2 seconds, the velocity makes an angle of 45° with the X-axis. This means:
Vx=Vy
Using the vertical motion equation again at t=2 seconds:
Vy=Uy−g⋅2
Substituting Uy=40:
Vy=40−20=20m/s
Since Vx=Vy:
Vx=20m/s
Now we have:
- Uy=40m/s
- Ux=Vx=20m/s
The magnitude of the initial velocity U can be calculated using the Pythagorean theorem:
U=√U2x+U2y
Substituting the values:
U=√(20)2+(40)2
U=√400+1600
U=√2000
U=20√5m/s
The velocity of projection is:
U=20√5m/s
Similar Questions
A particle is projected in the x-y plane with y-axis along vertical. Two second after projection the velocity of the particle makers an angle 45∘ with the X-axis. Four second after projection. It moves horizontally. Find velocity of projection.
View SolutionA particle is projected with a speed u. If after 2 seconds of projection it is found to be making an angle of 45∘ with the horizontal and 0∘ after 3 sec, then:
View SolutionOne second after the projection, a stone moves at an angle of 45∘ with the horizontal. Two seconds from the start,
it is travelling horizontally. Find the angle of projection with the horizontal. (g=10ms−2).
View SolutionA ball is projected from the ground at angle θ with the horizontal. After 1s, it is moving at angle 45∘ with the horizontal and after 2s it is moving horizontally. What is the velocity of projection of the ball ?
View SolutionA particle is projected with velocity V for point O of particle makes 10 revolutions before coming out. Find l.
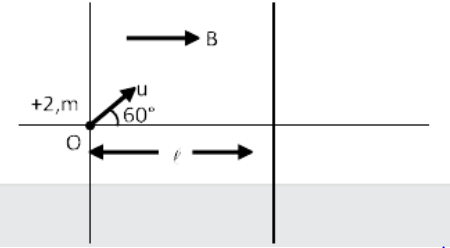
View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View SolutionA particle is projected with a speed 10√2 making an angle 45∘ with the horizontal . Neglect the effect of air friction. Then after 1 second of projection . Take g=10m/s2.
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
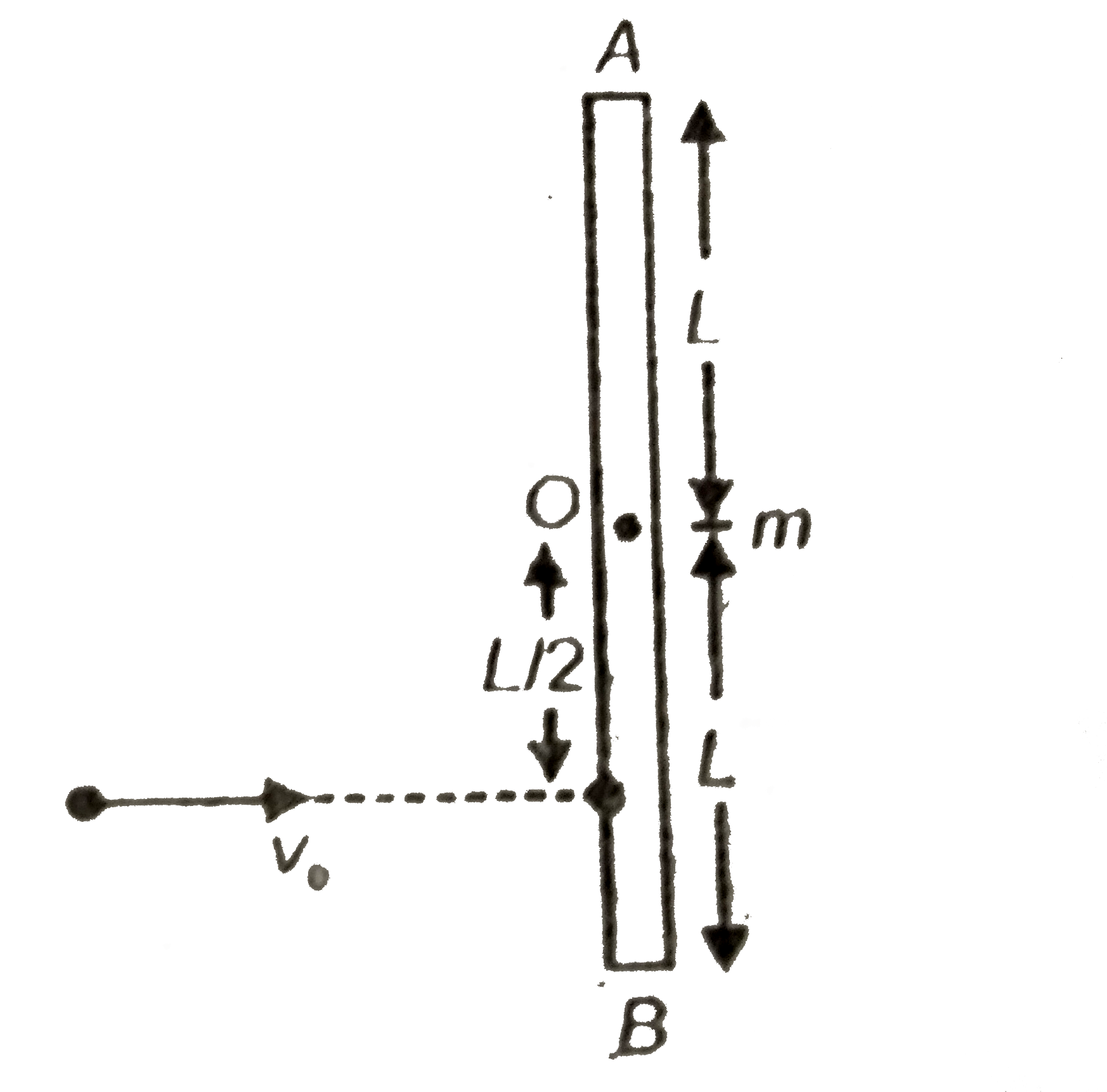
Distance of point P on rod from B which is at rest immediately afte collision is
View Solution
