A particle is projected with velocity V for point O of particle makes 10 revolutions before coming out. Find l. 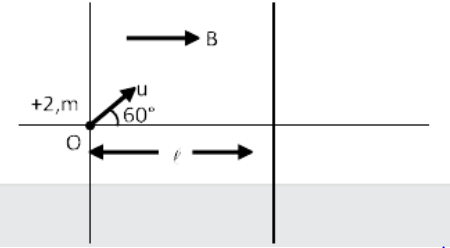
(πmvqB)
(2πmvqB)
(10πmvqB)
(40πmvqB)
The correct Answer is:C
Step by step video & image solution for A particle is projected with velocity V for point O of particle makes 10 revolutions before coming out. Find l. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle P is projected upwards with 80m/s. One second later another particle Q is projected with initial velocity 70m/s. Before either of the particle srikes the ground (g=10m/s2)
View SolutionA particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.

View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA particle projected with velcoity v0 strikes at right α plane through the point of projection .
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
View SolutionA particle is projected in the X−Y plane. 2sec after projection the velocity of the particle makes an angle 45∘ with the X−axis. 4sec after projection, it moves horizontally. Find the velocity of projection (use g=10ms−2).
View SolutionA particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
View SolutionA particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View Solution
