A uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
the centre of rod follows straight line path
the centre mass follows circular path
the instantaneous axis is passing through the contact point
all of above
The correct Answer is:A
To solve the problem step by step, we need to analyze the motion of the uniform straight rod when it is released from a vertical position on a smooth horizontal surface.
Step 1: Understand the Initial Setup
- A uniform straight rod of length L is placed vertically on a smooth horizontal surface.
- The center of mass of the rod is located at a distance of L2 from the base of the rod.
Hint: Visualize the rod standing vertically with its center of mass at the midpoint.
Step 2: Identify Forces Acting on the Rod
- The only force acting on the rod is its weight, which is mg (where m is the mass of the rod and g is the acceleration due to gravity).
- Since the surface is smooth, there is no friction acting on the rod.
Hint: Remember that the absence of friction means there is no horizontal force acting on the rod.
Step 3: Analyze the Motion of the Rod
- When the rod is released, it will start to fall due to gravity.
- The center of mass of the rod will move downward as the rod falls.
Hint: Consider the motion of the center of mass as if it were a particle falling under the influence of gravity.
Step 4: Determine the Path of the Center of Mass
- As the rod falls, the center of mass will follow a straight vertical path downward.
- This is because the rod is not experiencing any horizontal forces, and thus the motion of the center of mass can be treated as free fall.
Hint: Think of the center of mass as a point mass falling freely under gravity.
Step 5: Conclusion
- The path followed by the center of mass of the rod is a straight line downward, similar to the motion of a freely falling object under gravity.
Final Answer: The path followed by the center of mass of the rod is a straight line.
- A uniform straight rod of length L is placed vertically on a smooth horizontal surface.
- The center of mass of the rod is located at a distance of L2 from the base of the rod.
- The only force acting on the rod is its weight, which is mg (where m is the mass of the rod and g is the acceleration due to gravity).
- Since the surface is smooth, there is no friction acting on the rod.
- When the rod is released, it will start to fall due to gravity.
- The center of mass of the rod will move downward as the rod falls.
- As the rod falls, the center of mass will follow a straight vertical path downward.
- This is because the rod is not experiencing any horizontal forces, and thus the motion of the center of mass can be treated as free fall.
- The path followed by the center of mass of the rod is a straight line downward, similar to the motion of a freely falling object under gravity.
Similar Questions
A uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
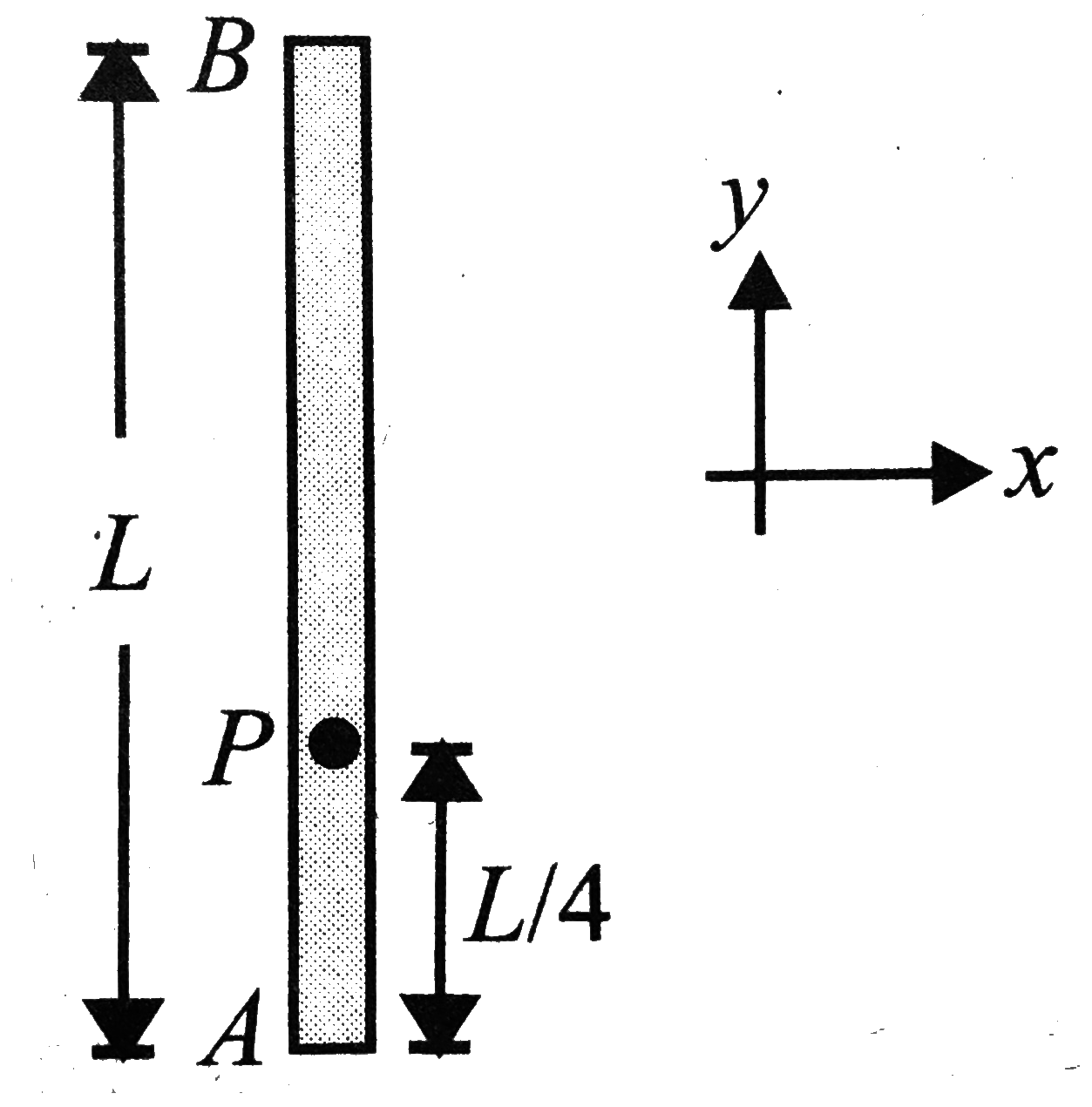
The acceleration of the centre of mass of the rod is
View SolutionA uniform rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

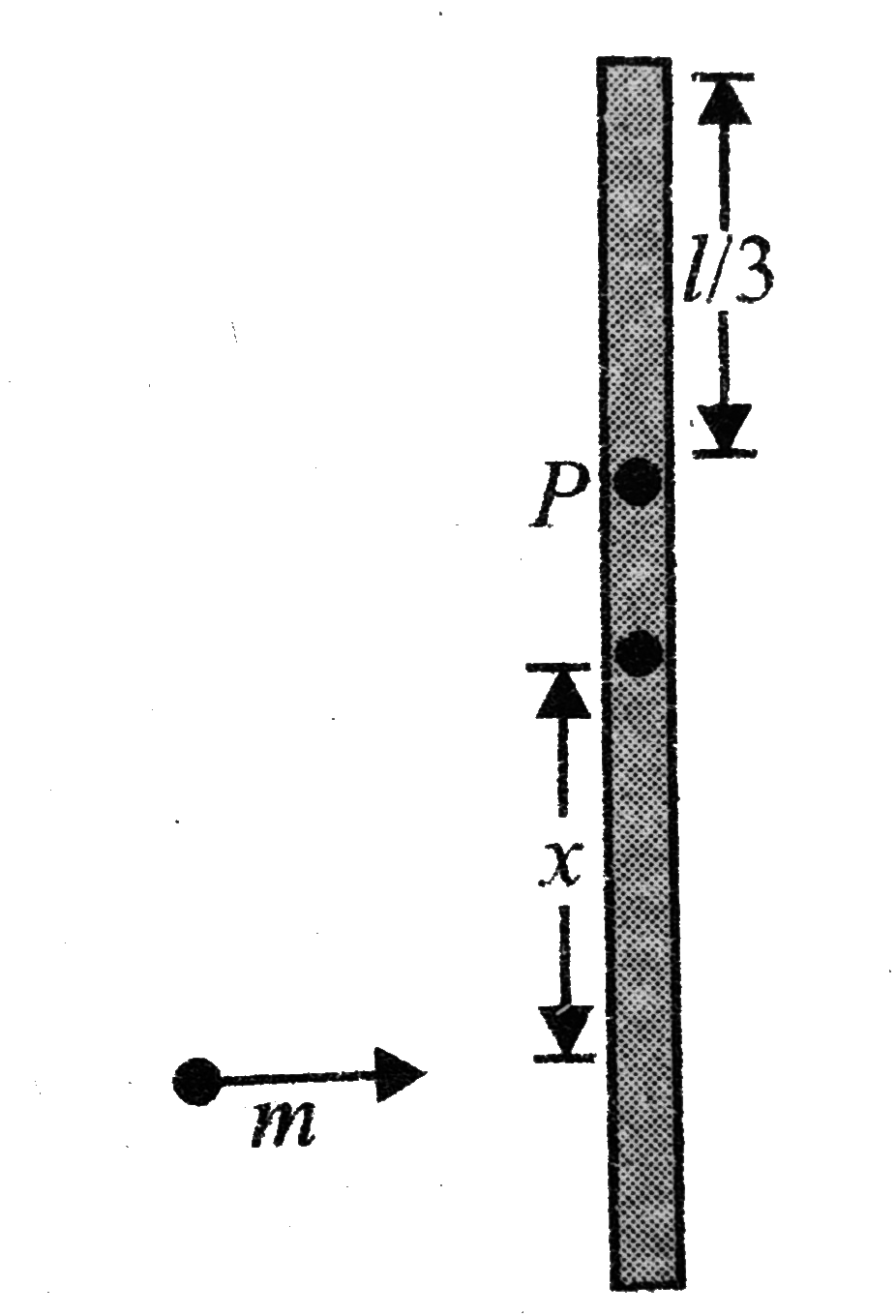
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
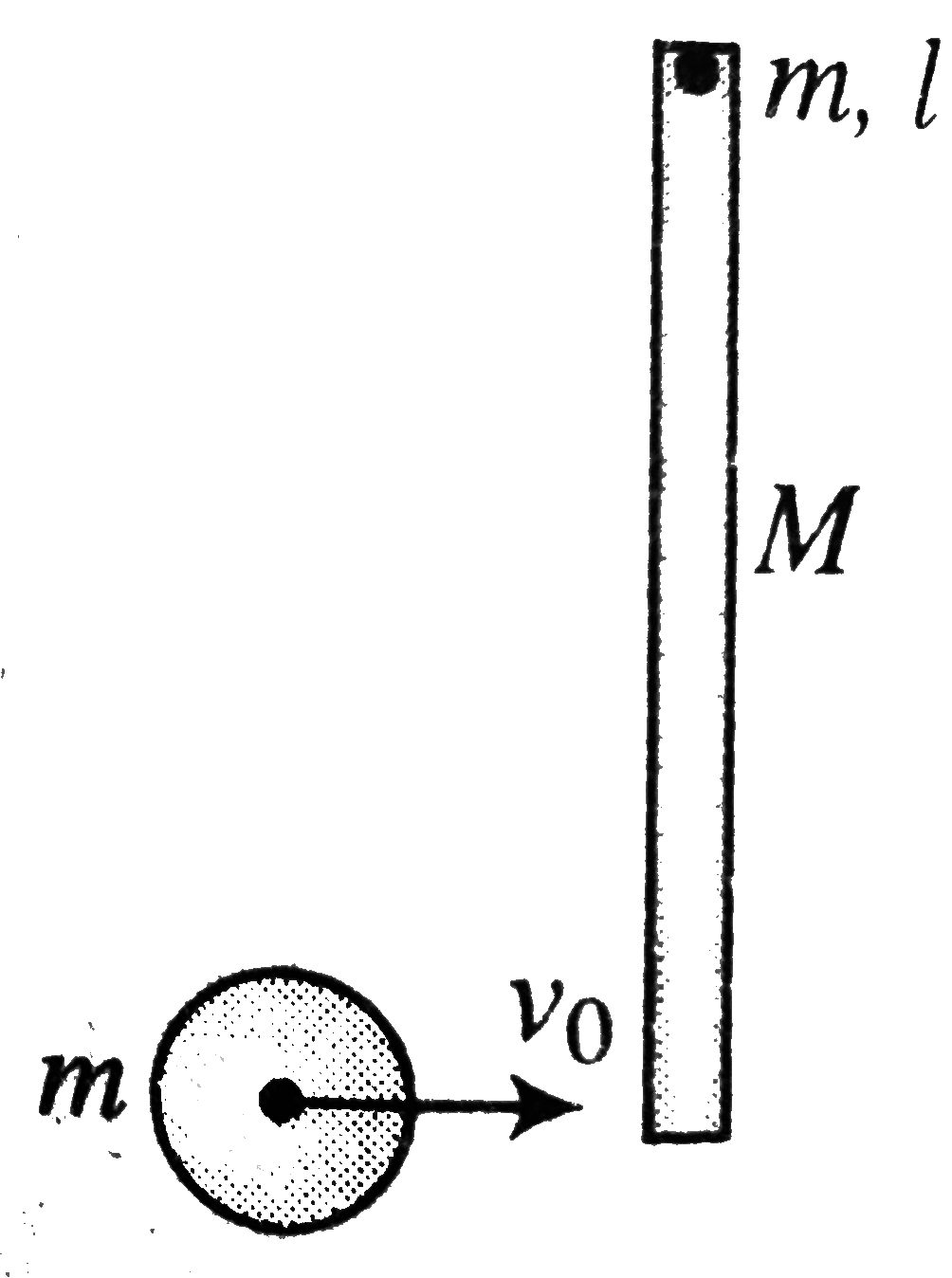
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA rod of length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle 37∘ with horizontal the velocity of COM of the rod of 2m/s. The velocity of the end of the rod in contact with the surface at that instant is
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View SolutionA uniform rod AB of mass 3m and length 4l, which is free to turn in a vertical plane about a smooth horizontal axis through A, is released from rest when horizontal. When the rod first becomes vertical, a point C of the rod, where AC=3l strikes a fixed peg. Find the linear impulse exerted by the peg on the rod if
(a). The rod is brought to rest by the peg.
(b). The rod rebounds and next comes to instantaneous rest inclined to the downward vertical at an angle π3 radian.
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View Solution