A particle of mass m1 makes a head - on elastic collision with another particle of mass m2 at rest. m1 rebounds straight back with 49 of its initial kinetic energy . Then m1m2 is :
23
15
32
25
The correct Answer is:B
To solve the problem step by step, we will analyze the elastic collision between two particles, one of which is initially at rest. We will use the principles of conservation of momentum and kinetic energy, along with the information given about the kinetic energy after the collision.
Step 1: Understand the Problem
We have two particles:
- Particle 1 (mass m1) is moving with initial velocity u1.
- Particle 2 (mass m2) is at rest, so its initial velocity u2=0.
After the collision, particle 1 rebounds with a velocity v1 and particle 2 moves with a velocity v2. We know that the kinetic energy of particle 1 after the collision is 49 of its initial kinetic energy.
Step 2: Write the Initial and Final Kinetic Energies
The initial kinetic energy KEinitial of particle 1 is given by:
KEinitial=12m1u21
The final kinetic energy KEfinal of particle 1 after the collision is:
KEfinal=12m1v21
According to the problem, we have:
KEfinal=49KEinitial
Substituting the expressions for kinetic energy, we get:
12m1v21=49(12m1u21)
Cancelling 12m1 from both sides (assuming m1≠0):
v21=49u21
Taking the square root:
v1=23u1
Step 3: Apply Conservation of Momentum
The conservation of momentum before and after the collision gives us:
m1u1+m2u2=m1v1+m2v2
Since u2=0, this simplifies to:
m1u1=m1v1+m2v2
Substituting v1=−23u1 (negative because it rebounds in the opposite direction):
m1u1=m1(−23u1)+m2v2
Rearranging gives:
m1u1+23m1u1=m2v2
53m1u1=m2v2(Equation 1)
Step 4: Use the Coefficient of Restitution
For elastic collisions, the coefficient of restitution e=1. This means:
e=v2+v1u1
Substituting v1=−23u1:
1=v2−23u1u1
This simplifies to:
v2−23u1=u1
Thus, we have:
v2=u1+23u1=53u1(Equation 2)
Step 5: Substitute Equation 2 into Equation 1
Now we substitute v2 from Equation 2 into Equation 1:
53m1u1=m2(53u1)
Cancelling 53u1 from both sides (assuming u1≠0):
m1=m2
Step 6: Find the Ratio m1m2
Thus, we can express the ratio of the masses:
m1m2=1
Conclusion
The final answer is:
m1m2=15
We have two particles:
- Particle 1 (mass m1) is moving with initial velocity u1.
- Particle 2 (mass m2) is at rest, so its initial velocity u2=0.
The initial kinetic energy KEinitial of particle 1 is given by:
KEinitial=12m1u21
The final kinetic energy KEfinal of particle 1 after the collision is:
KEfinal=12m1v21
According to the problem, we have:
KEfinal=49KEinitial
Substituting the expressions for kinetic energy, we get:
12m1v21=49(12m1u21)
Cancelling 12m1 from both sides (assuming m1≠0):
v21=49u21
Taking the square root:
v1=23u1
The conservation of momentum before and after the collision gives us:
m1u1+m2u2=m1v1+m2v2
Since u2=0, this simplifies to:
m1u1=m1v1+m2v2
Substituting v1=−23u1 (negative because it rebounds in the opposite direction):
m1u1=m1(−23u1)+m2v2
Rearranging gives:
m1u1+23m1u1=m2v2
53m1u1=m2v2(Equation 1)
For elastic collisions, the coefficient of restitution e=1. This means:
e=v2+v1u1
Substituting v1=−23u1:
1=v2−23u1u1
This simplifies to:
v2−23u1=u1
Thus, we have:
v2=u1+23u1=53u1(Equation 2)
Now we substitute v2 from Equation 2 into Equation 1:
53m1u1=m2(53u1)
Cancelling 53u1 from both sides (assuming u1≠0):
m1=m2
Thus, we can express the ratio of the masses:
m1m2=1
The final answer is:
m1m2=15
Similar Questions
A particle of mass m1, makes a head on elastic collision with another stationary body of mass m2 If m1, rebounds with half of its original speed then (m1m2) is
View SolutionAn alpha-particle of mass m suffers 1-dimentinal eleastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing 64% of its initial kinetic energy. The mass of the nucleus is :
View Solution
Knowledge Check
A spherical ball of mass m1 collides head on with another ball of mass m2 at rest . The collision is elastic . The fraction of kinetic energy lost by m1 is :
A4m1m2(m1+m2)2Bm1m1+m2Cm2m1+m2Dm1m2(m1+m2)2
A particle moving with kinetic energy E makes a head on elastic collision with an identical particle at rest. During the collision
View SolutionA particle of mass m is moving along the x-axis with initial velocity ui . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
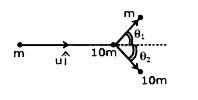
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionA moving body of mass m makes a head on elastic collision with another body of mass 2m which is initially at rest. Find the fraction of kinetic energy lost by the colliding particles after collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View Solution
