An alpha-particle of mass m suffers 1-dimentinal eleastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing 64% of its initial kinetic energy. The mass of the nucleus is :
2 m
3.5 m
1.5 m
4 m
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have an alpha particle of mass m colliding elastically with a nucleus of unknown mass M that is initially at rest. After the collision, the alpha particle is scattered directly backward and loses 64% of its initial kinetic energy.
Step 2: Determine the initial kinetic energy of the alpha particle
The initial kinetic energy KEi of the alpha particle is given by:
KEi=12mu2
where u is the initial velocity of the alpha particle.
Step 3: Calculate the final kinetic energy of the alpha particle
Since the alpha particle loses 64% of its kinetic energy, it retains 36% of its initial kinetic energy:
KEf=0.36×KEi=0.36×12mu2
Step 4: Express the final kinetic energy in terms of the final velocity
Let v1 be the final velocity of the alpha particle after the collision. The final kinetic energy can also be expressed as:
KEf=12mv21
Setting the two expressions for KEf equal gives:
12mv21=0.36×12mu2
We can cancel 12m from both sides (assuming m≠0):
v21=0.36u2
Taking the square root:
v1=0.6u
Step 5: Apply conservation of momentum
Before the collision, the total momentum is:
pi=mu+0=mu
After the collision, the momentum is:
pf=−mv1+Mv2
where v2 is the velocity of the nucleus after the collision. Setting the initial momentum equal to the final momentum gives:
mu=−m(0.6u)+Mv2
This simplifies to:
mu=−0.6mu+Mv2
Rearranging gives:
mu+0.6mu=Mv2
1.6mu=Mv2
Step 6: Use the coefficient of restitution
For elastic collisions, the coefficient of restitution e=1 gives us:
v2+v1=u
Substituting v1=0.6u:
v2+0.6u=u
Solving for v2:
v2=u−0.6u=0.4u
Step 7: Substitute v2 back into the momentum equation
Now we substitute v2=0.4u back into the momentum equation:
1.6mu=M(0.4u)
Cancelling u (assuming u≠0):
1.6m=0.4M
Solving for M:
M=1.6m0.4=4m
Conclusion
The mass of the nucleus is 4m.
We have an alpha particle of mass m colliding elastically with a nucleus of unknown mass M that is initially at rest. After the collision, the alpha particle is scattered directly backward and loses 64% of its initial kinetic energy.
The initial kinetic energy KEi of the alpha particle is given by:
KEi=12mu2
where u is the initial velocity of the alpha particle.
Since the alpha particle loses 64% of its kinetic energy, it retains 36% of its initial kinetic energy:
KEf=0.36×KEi=0.36×12mu2
Let v1 be the final velocity of the alpha particle after the collision. The final kinetic energy can also be expressed as:
KEf=12mv21
Setting the two expressions for KEf equal gives:
12mv21=0.36×12mu2
We can cancel 12m from both sides (assuming m≠0):
v21=0.36u2
Taking the square root:
v1=0.6u
Before the collision, the total momentum is:
pi=mu+0=mu
After the collision, the momentum is:
pf=−mv1+Mv2
where v2 is the velocity of the nucleus after the collision. Setting the initial momentum equal to the final momentum gives:
mu=−m(0.6u)+Mv2
This simplifies to:
mu=−0.6mu+Mv2
Rearranging gives:
mu+0.6mu=Mv2
1.6mu=Mv2
For elastic collisions, the coefficient of restitution e=1 gives us:
v2+v1=u
Substituting v1=0.6u:
v2+0.6u=u
Solving for v2:
v2=u−0.6u=0.4u
Now we substitute v2=0.4u back into the momentum equation:
1.6mu=M(0.4u)
Cancelling u (assuming u≠0):
1.6m=0.4M
Solving for M:
M=1.6m0.4=4m
The mass of the nucleus is 4m.
Similar Questions
A particle of mass m1 makes a head - on elastic collision with another particle of mass m2 at rest. m1 rebounds straight back with 49 of its initial kinetic energy . Then m1m2 is :
View SolutionA particle of mass m has momentum p. Its kinetic energy will be
View SolutionA particle A suffers an oblique elastic collision particle B that is at rest initially. If their masses with a are the same, then after the collision
View SolutionA moving body of mass m makes a head on elastic collision with another body of mass 2m which is initially at rest. Find the fraction of kinetic energy lost by the colliding particles after collision.
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionA particle of mass m is moving along the x-axis with initial velocity ui . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
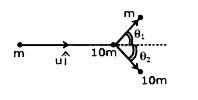
View SolutionA body of mass 2 m moving with velocity v makes a head - on elastic collision with another body of mass m which is initially at rest. Loss of kinetic energy of the colliding body (mass 2 m) is
View SolutionA particle loses 25% of its energy during collision with another identical particle at rest. the coefficient of restitution will be
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass 220meV/c2 collides with a hydrogen tom at rest. Soon after the collisionthe particle comes to rest, and the atom recoils and goes to its first excited state. The initial kinetic energy of the particle (in eV) is N4. The value of N is :
(Given the mass of the hydrogen atom to be 1GeV/c2)_____________
View Solution
