The ratio of energies of emitted radiation by a black body at 600 K and 900 K , when the surrounding temperature is 300 K , is
516
716
316
916
The correct Answer is:C
To solve the problem of finding the ratio of energies of emitted radiation by a black body at temperatures of 600 K and 900 K, with a surrounding temperature of 300 K, we can follow these steps:
1. Understand the Stefan-Boltzmann Law: The energy emitted by a black body is proportional to the fourth power of its absolute temperature. Mathematically, this is expressed as:
E∝T4
2. Consider the Surrounding Temperature: Since the black body is not in a vacuum, we need to account for the surrounding temperature (Ts = 300 K). The effective energy emitted by the black body is given by:
E=σ(T4−T4s)
where σ is the Stefan-Boltzmann constant.
3. Set Up the Ratio of Energies: Let E1 be the energy emitted at 600 K and E2 be the energy emitted at 900 K. We can express these as:
E1=σ(T41−T4s)=σ(6004−3004)
E2=σ(T42−T4s)=σ(9004−3004)
4. Form the Ratio: The ratio of the energies emitted can be expressed as:
E1E2=6004−30049004−3004
5. Calculate the Values:
- First, calculate 6004:
6004=129600000000
- Next, calculate 3004:
3004=8100000000
- Now, calculate 9004:
9004=656100000000
6. Substitute the Values:
- Substitute these values into the ratio:
E1E2=129600000000−8100000000656100000000−8100000000
- This simplifies to:
E1E2=121500000000648900000000
7. Simplify the Ratio:
- Divide both the numerator and denominator by 121500000000:
E1E2=15.35≈316
8. Final Result: Thus, the ratio of energies emitted by the black body at 600 K and 900 K is:
E1E2=316
Conclusion:
The required ratio of energies emitted by the black body at 600 K and 900 K, when the surrounding temperature is 300 K, is 316.
E∝T4
E=σ(T4−T4s)
where σ is the Stefan-Boltzmann constant.
E1=σ(T41−T4s)=σ(6004−3004)
E2=σ(T42−T4s)=σ(9004−3004)
E1E2=6004−30049004−3004
- First, calculate 6004:
6004=129600000000
- Next, calculate 3004:
3004=8100000000
- Now, calculate 9004:
9004=656100000000
- Substitute these values into the ratio:
E1E2=129600000000−8100000000656100000000−8100000000
- This simplifies to:
E1E2=121500000000648900000000
- Divide both the numerator and denominator by 121500000000:
E1E2=15.35≈316
E1E2=316
The required ratio of energies emitted by the black body at 600 K and 900 K, when the surrounding temperature is 300 K, is 316.
Similar Questions
The ratio of energy of emitted radiation of black body at 27∘Cand927∘c is
View SolutionIn the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
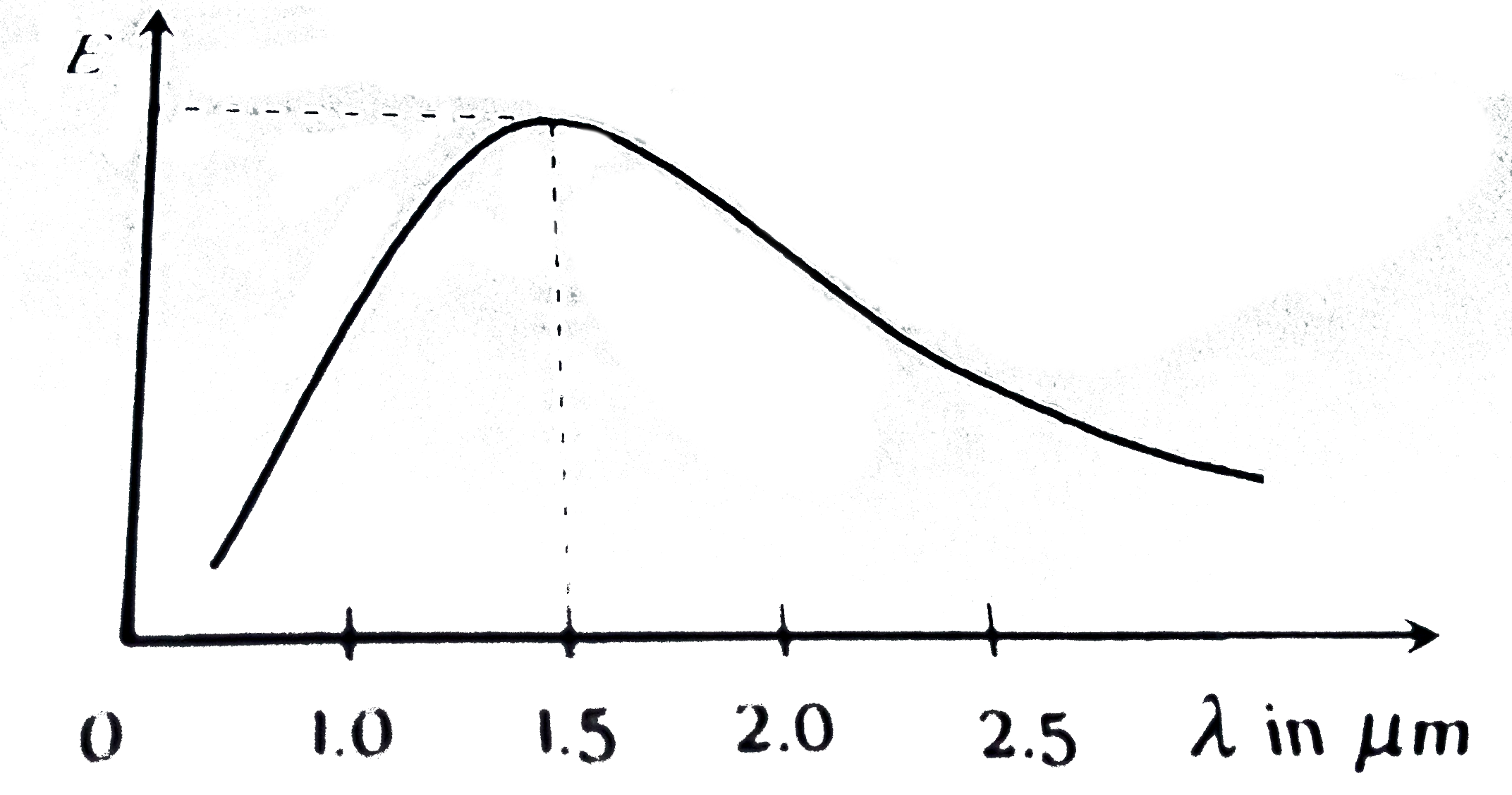
View SolutionOne end of a rod of length 20cm is inserted in a furnace at 800K The sides of the rod are covered with an insulating material and the other end emits radiation like a black body. The temperature of this end is 750K in the steady state The temperature of the surrounding air is 300K Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod Stefan's constant σ=6.0×10−8Wm−2K−4 .
View SolutionA wire of length 1 m and radius 10−3m is carrying a heavy current and is assumed to radiate as a black body. At equilibrium, its temperature is 900 K while that of surrounding is 300 K. The resistivity of the material of the wire at 300 K is π∘×10−8 ohm m and its temperature coefficient of resistance is 7.8×10−3/C (stefan's constantσ=5.68×10−8W/m2K4).
Q. The resistivity of wire at 900 K is nearly
View SolutionA wire of length 1 m and radius 10−3m is carrying a heavy current and is assumed to radiate as a black body. At equilibrium, its temperature is 900 K while that of surrounding is 300 K. The resistivity of the material of the wire at 300 K is π∘×10−8 ohm m and its temperature coefficient of resistance is 7.8×10−3/C (stefan's constantσ=5.68×10−8W/m2K2.
Heat radiated per second by the wire is nearly
View SolutionA wire of length 1 m and radius 10−3m is carrying a heavy current and is assumed to radiate as a black body. At equilibrium, its temperature is 900 K while that of surrounding is 300 K. The resistivity of the material of the wire at 300 K is π∘×10−8 ohm m and its temperature coefficient of resistance is 7.8×10−3/C (stefan's constantσ=5.68×10−8W/m2K2.
The current in the wire is nearly
View SolutionOne end of a rod length 20cm is inserted in a furnace at 800K. The sides of the rod are covered with an insulating material and the other end emits radiation like a blackbody. The temperature of this end is 750K in the steady state. The temperature of the surrounding air is 300K. Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod. Stefan constant σ=6.0×10−1Wm−2K−4 .
View SolutionOne end of a rod length 20cm is inserted in a furnace at 800K. The sides of the rod are covered with an insulating material and the other end emits radiation like a blackbody. The temperature of this end is 750K in the steady state. The temperature of the surrounding air is 300K. Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod. Stefan constant σ=6.0×10−1Wm−2K−4 .
View SolutionParallel rays of light of intensity I=912WM−2 are incident on a spherical black body kept in surroundings of temperature 300K. Take Stefan-Boltzmann constant σ=5.7×10−8
Wm−2K−4 and assume that the energy exchange with the surroundings is only through radiation. The final steady state temperature of the black body is close to
View SolutionThe energy radiated by a black body is directly proportional to :
View Solution
