The ratio of energy of emitted radiation of black body at 27∘Cand927∘c is
1:256
1:64
1:16
1:4
The correct Answer is:A
To find the ratio of the energy of emitted radiation of a black body at temperatures of 27°C and 927°C, we can use the Stefan-Boltzmann law, which states that the power (energy per unit time) emitted by a black body is proportional to the fourth power of its absolute temperature (in Kelvin).
1. Convert Celsius to Kelvin:
- The temperature in Kelvin (K) is given by the formula:
T(K)=T(°C)+273
- For the first temperature (27°C):
T1=27+273=300K
- For the second temperature (927°C):
T2=927+273=1200K
2. Apply the Stefan-Boltzmann Law:
- The power emitted by a black body is given by:
P∝T4
- Therefore, the ratio of the powers emitted at the two temperatures can be expressed as:
P1P2=(T1T2)4
3. Substitute the Temperatures:
- Substitute T1=300K and T2=1200K:
P1P2=(3001200)4
4. Simplify the Ratio:
- Simplifying the fraction:
3001200=14
- Now raise this to the power of 4:
(14)4=1256
5. Final Result:
- Thus, the ratio of the energy emitted at 27°C to that at 927°C is:
P1P2=1256
Conclusion:
The ratio of energy of emitted radiation of a black body at 27°C and 927°C is 1256.
- The temperature in Kelvin (K) is given by the formula:
T(K)=T(°C)+273
- For the first temperature (27°C):
T1=27+273=300K
- For the second temperature (927°C):
T2=927+273=1200K
- The power emitted by a black body is given by:
P∝T4
- Therefore, the ratio of the powers emitted at the two temperatures can be expressed as:
P1P2=(T1T2)4
- Substitute T1=300K and T2=1200K:
P1P2=(3001200)4
- Simplifying the fraction:
3001200=14
- Now raise this to the power of 4:
(14)4=1256
- Thus, the ratio of the energy emitted at 27°C to that at 927°C is:
P1P2=1256
The ratio of energy of emitted radiation of a black body at 27°C and 927°C is 1256.
Similar Questions
The ratio of energies of emitted radiation by a black body at 600 K and 900 K , when the surrounding temperature is 300 K , is
View SolutionThe rate of radiation of a black body at 0° C is E . The rate of radiation of this black body at 273∘C will be
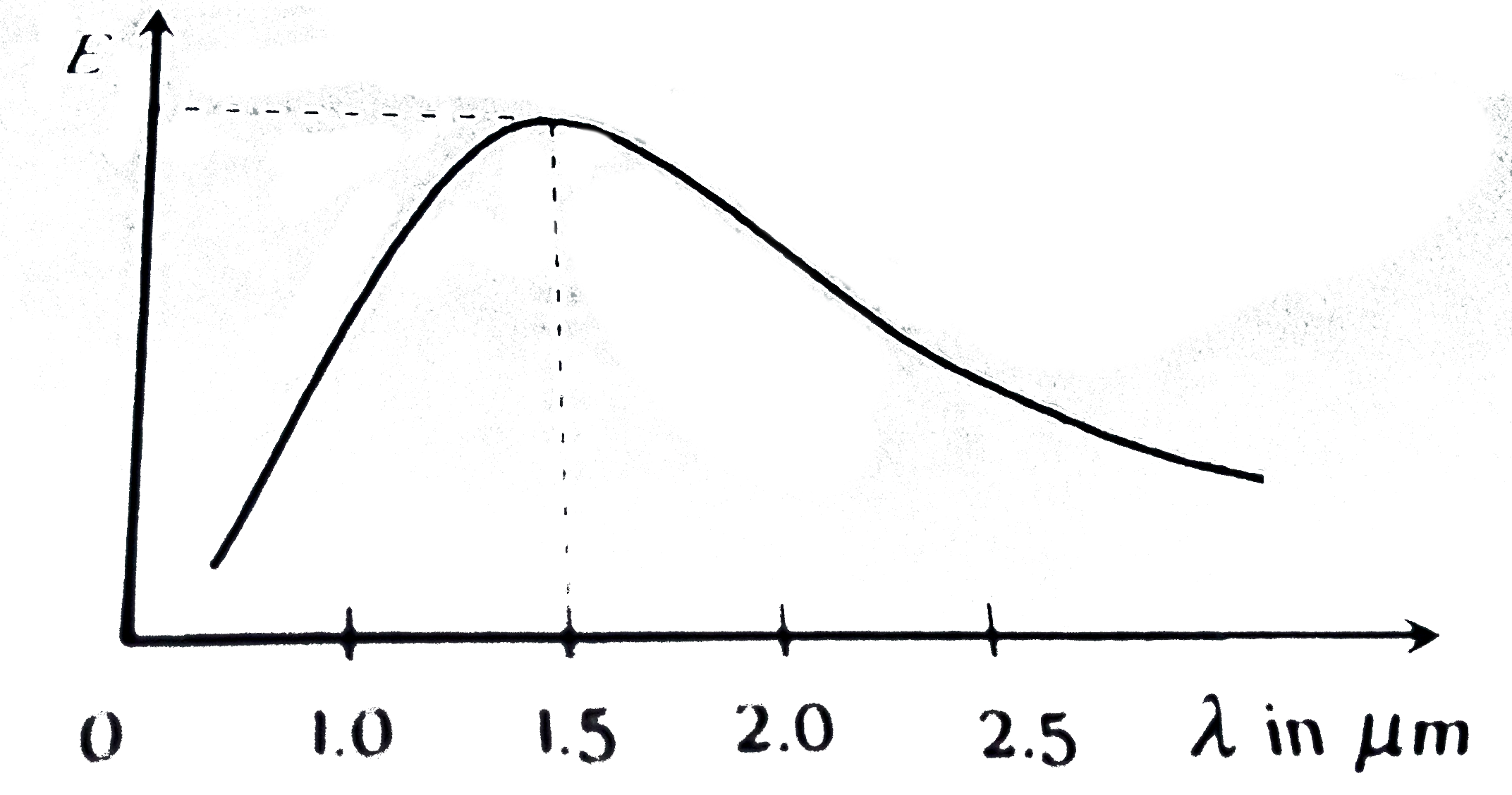
View SolutionIn the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
View SolutionA heated body maitained at T K emits thermal radiation of total energy E with a maximum intensity at frequency v. The emissivity of the material is 0.5. If the temperature of the body be increased and maintained at temperature 3T K, then :-
(i) The maximum intensity of the emitted radiation will occur at frequency v/3
(ii) The maximum intensity of the emitted radiation will occur at frequency 3v.
(iii) The total energy of emitted radiation will become 81 E
(iv) The total energy of emitted radiation will become 27 E
View SolutionCalculate the amount of radiant energy from a black body at a temperature of (i) 27∘C (ii) 2727∘C. σ=5.67×10−8Wm−2K−4.
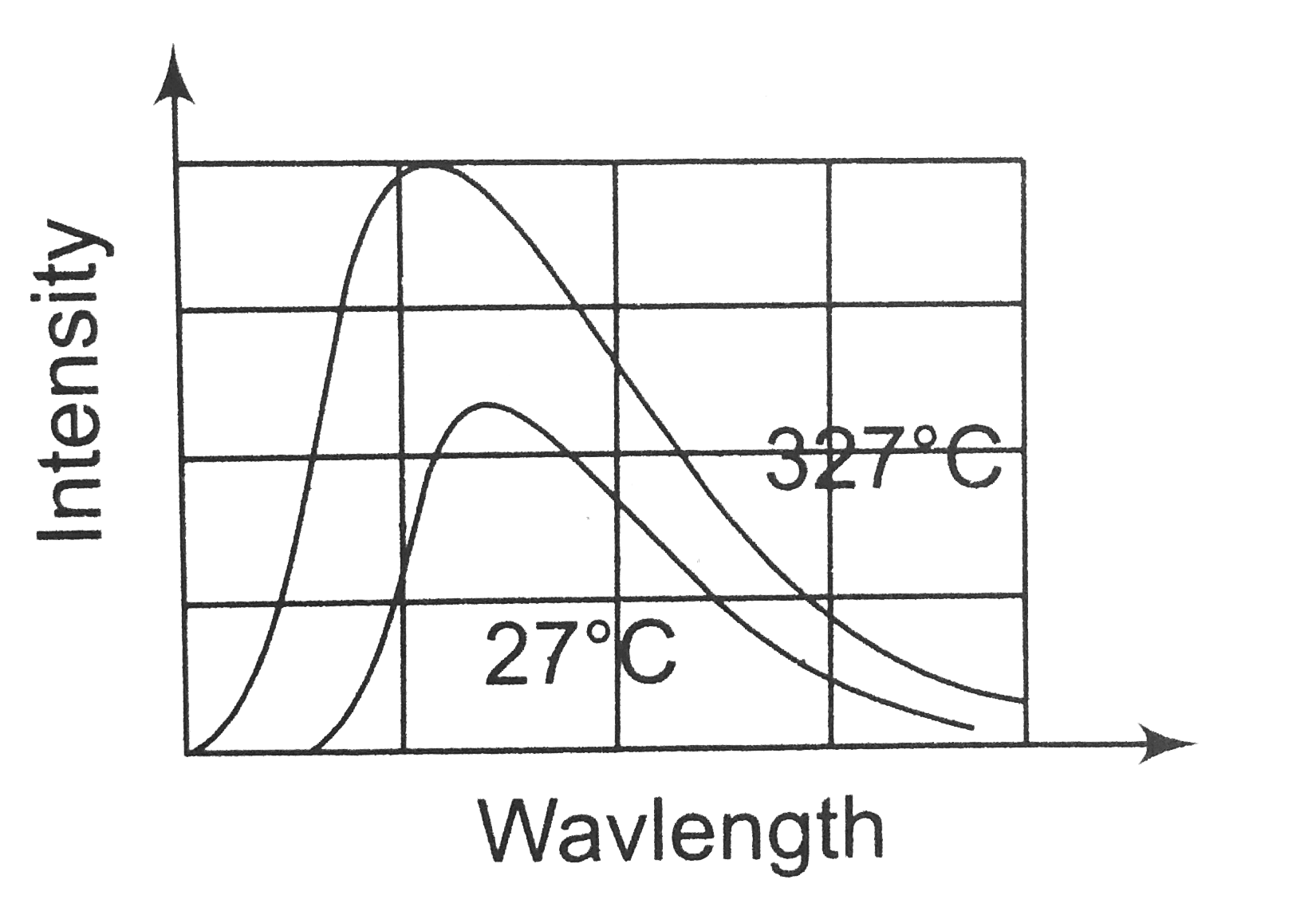
View SolutionThe spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
View SolutionFind the efficiency of carnot engine whose source and sink are at 927∘C and 27∘C.
View SolutionFind the efficiency of carnot engine whose source and sink are at 927∘C and 27∘C.
View SolutionDoes a body at 0∘C radiate any heat ?
View SolutionThe ratio of the energy of a photon of 200Å wavelength radiation to that of 400Å radiation is :
View Solution
