A particle moves along a straight line path. After some time it comes to rest. The motion is with constant acceleration whose direction with respect to the direction of velocity is :
positive throughout motion
negative throughout motion
first positive then negative
first negative then negative
The correct Answer is:B
To solve the problem, we need to analyze the motion of a particle that moves along a straight line and comes to rest under constant acceleration. Here's a step-by-step solution:
Step 1: Understand the Motion
The particle is initially moving with some velocity (let's denote it as Vi) and eventually comes to rest, meaning its final velocity (Vf) is 0.
Step 2: Use the Equation of Motion
Since the particle is moving with constant acceleration, we can use the equation of motion:
Vf=Vi+a⋅t
where:
- Vf = final velocity (0, since the particle comes to rest)
- Vi = initial velocity
- a = acceleration
- t = time
Step 3: Rearranging the Equation
Rearranging the equation gives us:
0=Vi+a⋅t
This can be rewritten as:
a⋅t=−Vi
From this, we can express acceleration as:
a=−Vit
Step 4: Analyze the Sign of Acceleration
Since Vi is positive (the particle is moving in the positive direction), and t is also positive (time cannot be negative), the acceleration a is negative. This indicates that the acceleration is in the opposite direction to the initial velocity.
Step 5: Conclusion
The direction of acceleration is opposite to the direction of velocity. Therefore, the acceleration is negative with respect to the direction of the velocity.
Final Answer
The direction of acceleration with respect to the direction of velocity is negative.
---
The particle is initially moving with some velocity (let's denote it as Vi) and eventually comes to rest, meaning its final velocity (Vf) is 0.
Since the particle is moving with constant acceleration, we can use the equation of motion:
Vf=Vi+a⋅t
where:
- Vf = final velocity (0, since the particle comes to rest)
- Vi = initial velocity
- a = acceleration
- t = time
Rearranging the equation gives us:
0=Vi+a⋅t
This can be rewritten as:
a⋅t=−Vi
From this, we can express acceleration as:
a=−Vit
Since Vi is positive (the particle is moving in the positive direction), and t is also positive (time cannot be negative), the acceleration a is negative. This indicates that the acceleration is in the opposite direction to the initial velocity.
The direction of acceleration is opposite to the direction of velocity. Therefore, the acceleration is negative with respect to the direction of the velocity.
The direction of acceleration with respect to the direction of velocity is negative.
Similar Questions
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
Velocity of a particle is in negative direction with constant acceleration in positive direction. Then match the following:

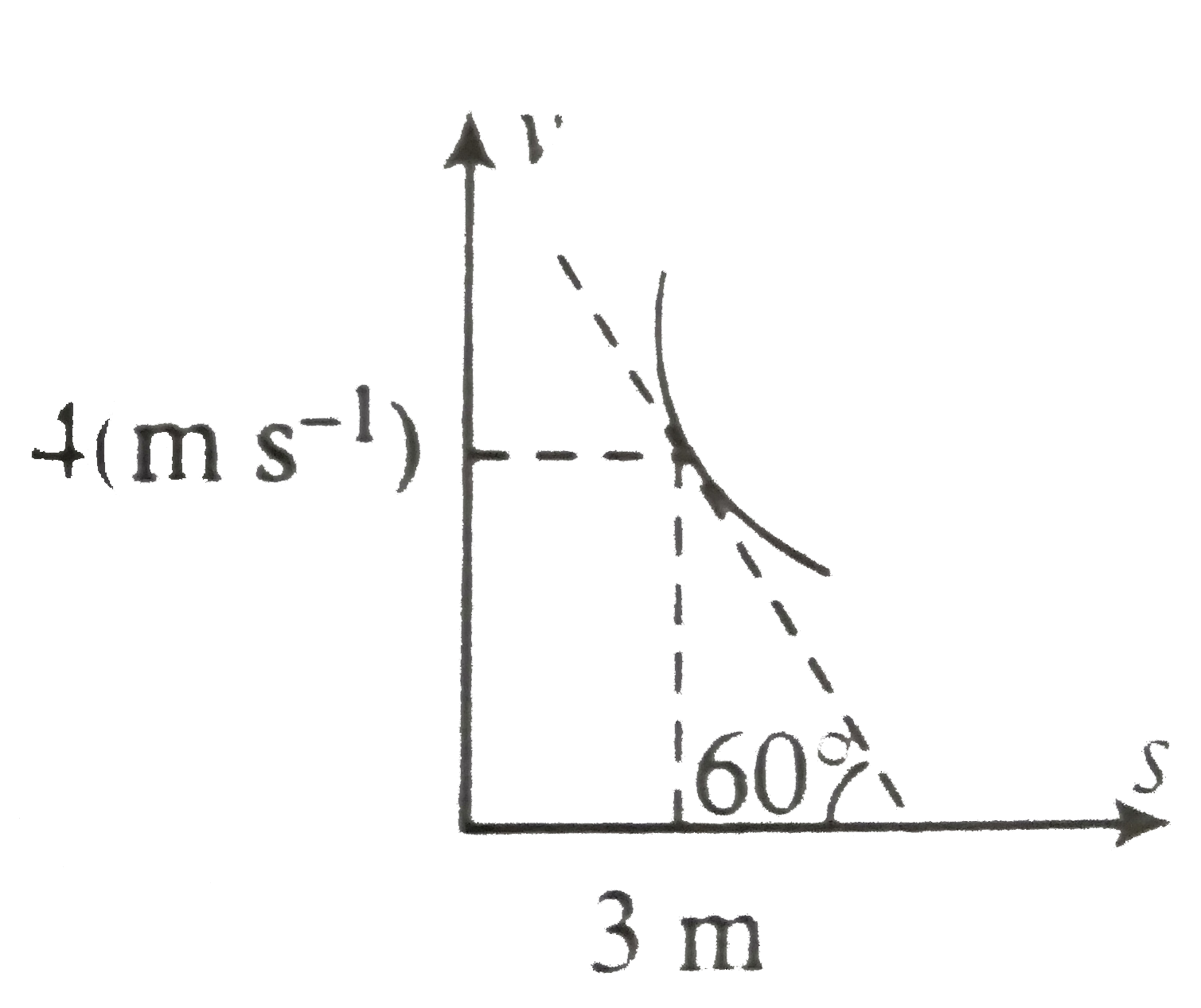
View SolutionA particle is moving along a straight line whose velocity - displacement graph is shown in figure. What is the acceleration when displacement is 3 m?
View SolutionA car moves in a straight line, the car accelerates from rest with a constant acceleraation α on a straight foad. After gaining a velocity v, the car moves with that velocity for somerime. Then car decelerates with a retardation β, If the total distance covered by the car is equal to s find the total time of its motion.
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:

View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View SolutionA particle starts from the origin of coordinates at time t = 0 and moves in the xy plane with a constant acceleration α in the y-direction. Its equation of motion is y=βx2. Its velocity component in the x-direction is
View SolutionThe velocity-time graph of a particle moving along a straight line is shown is Fig. The rate of acceleration and deceleration is constant and it is equal to 5ms−2. If the a average velocity during the motion is 20ms−1, Then
 .
.
The maximum velocity of the particle is .
View Solution
