A particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-

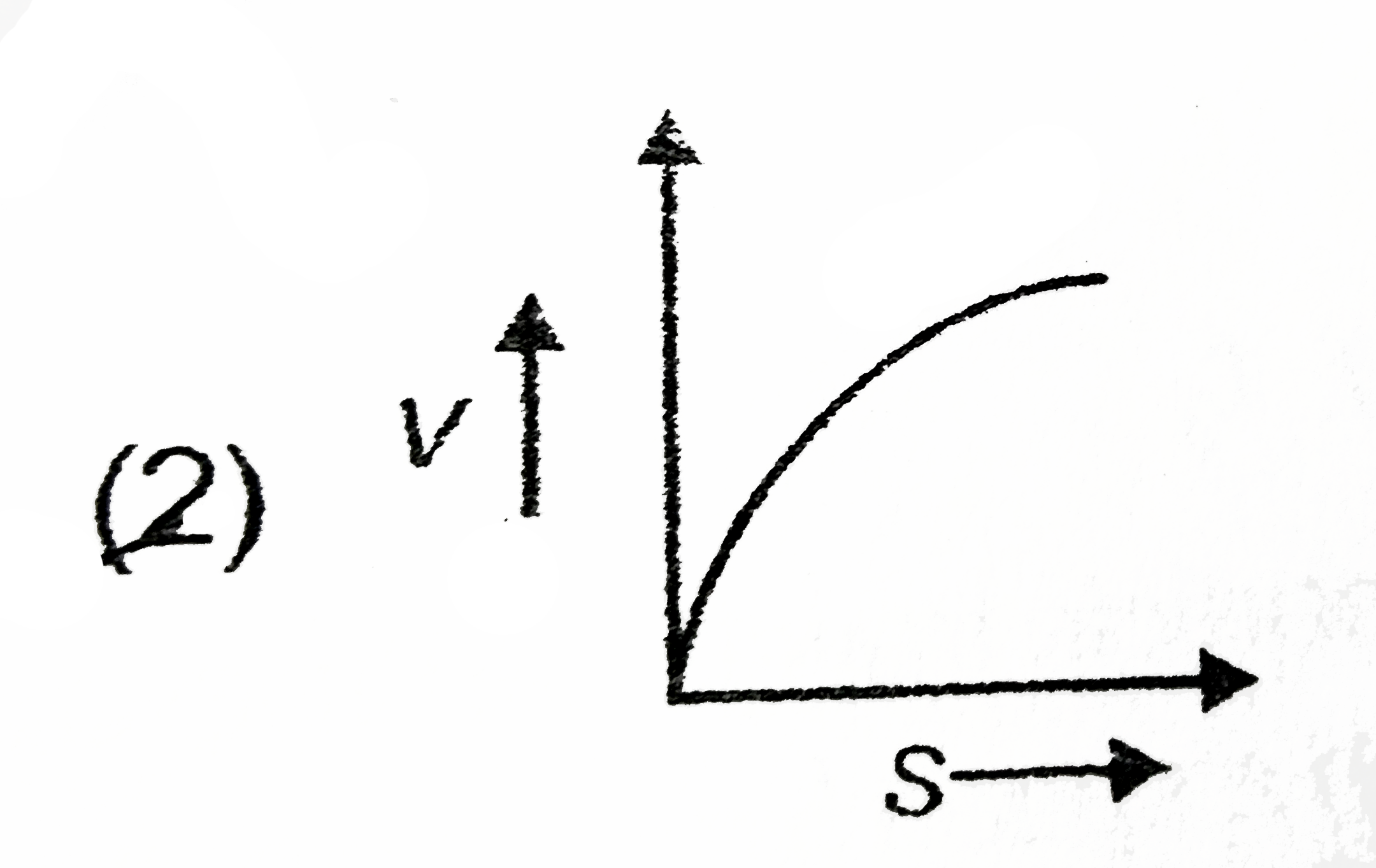


The correct Answer is:B
To solve the problem of determining the form of the velocity-displacement graph for a particle starting from rest and moving with constant acceleration, we can follow these steps:
Step 1: Understand the given conditions
The particle starts from rest, which means its initial velocity (u) is 0. It moves with constant acceleration (a).
Hint: Remember that "starting from rest" means the initial velocity is zero.
Step 2: Use the kinematic equation
For a particle moving with constant acceleration, we can use the kinematic equation that relates velocity (v), initial velocity (u), acceleration (a), and displacement (s):
v2=u2+2as
Since the initial velocity u=0, the equation simplifies to:
v2=2as
Hint: Identify the variables in the equation: v is the final velocity, a is acceleration, and s is displacement.
Step 3: Rearranging the equation
From the equation v2=2as, we can express s in terms of v:
s=v22a
This shows that displacement s is proportional to the square of the velocity v2.
Hint: Look for the relationship between s and v to determine the shape of the graph.
Step 4: Identify the type of graph
The equation s=12av2 indicates that s is proportional to v2. This means that if we plot v2 on the y-axis against s on the x-axis, we will get a straight line. However, if we plot v against s, the graph will be parabolic because s is proportional to v2.
Hint: Consider how the graph would look if you plotted v against s based on the relationship derived.
Step 5: Conclusion
Since the velocity v is related to the displacement s by a quadratic relationship, the velocity-displacement graph will be parabolic.
Thus, the correct answer is that the velocity-displacement graph will have the form of a parabola.
Final Answer: The velocity-displacement graph will be parabolic.
---
The particle starts from rest, which means its initial velocity (u) is 0. It moves with constant acceleration (a).
For a particle moving with constant acceleration, we can use the kinematic equation that relates velocity (v), initial velocity (u), acceleration (a), and displacement (s):
v2=u2+2as
Since the initial velocity u=0, the equation simplifies to:
v2=2as
From the equation v2=2as, we can express s in terms of v:
s=v22a
This shows that displacement s is proportional to the square of the velocity v2.
The equation s=12av2 indicates that s is proportional to v2. This means that if we plot v2 on the y-axis against s on the x-axis, we will get a straight line. However, if we plot v against s, the graph will be parabolic because s is proportional to v2.
Since the velocity v is related to the displacement s by a quadratic relationship, the velocity-displacement graph will be parabolic.
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - B)
19 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Try Yourself
40 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
Knowledge Check
A particle starts from point A moves along a straight line path with an acceleration given by a = p - qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qp
A particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q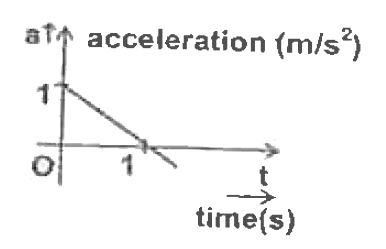
View SolutionA particle starts from origin and moves on a straight line path with an acceleration proportional to square of its displacement.Kinetic energy during displacement x will be
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionA particle is moving along a straight line with constant acceleration. At the end of tenth second its velocity becomes 20m/s and tenth second it travels a distance od 10m. Then the acceleration of the particle will be.
View SolutionThe velocity - displacement graph of a particle moving along a straight line is shown
The most suitable acceleration - displacement graph will be

View SolutionFigure shows acceleration versus time graph of a particle starting from rest and moving along a straight line. Which of the following staement (s) is/are correct ?
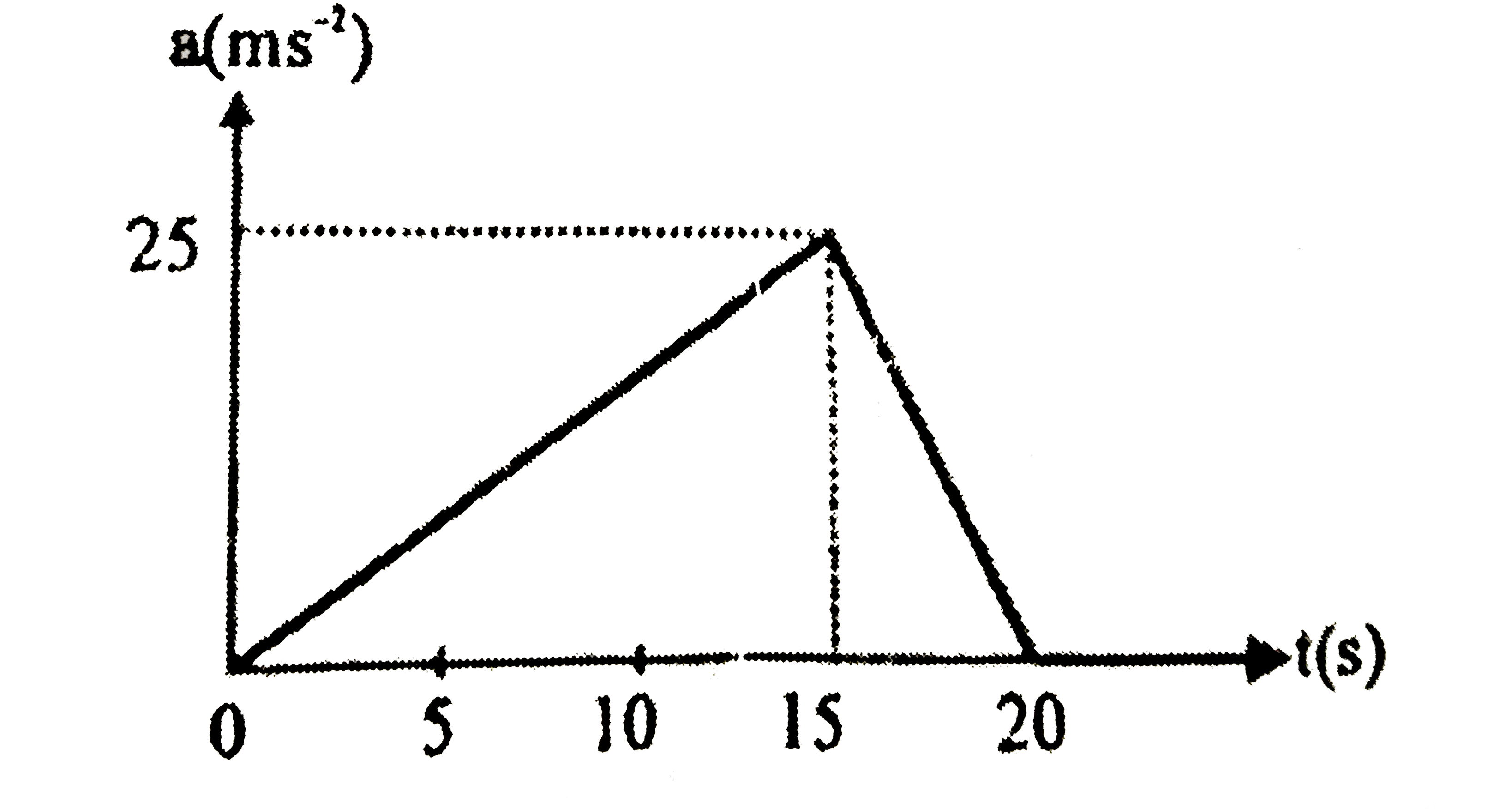
View Solution