Three identical spheres lie at rest along a line on a smooth horizontal surface. The separation between any two adjacent spheres is L. The first sphere is moving with a velocity u towards the second sphere at time t = 0. The coefficient of restitution for a collision between any two blocks is 13 The correct statement is
The third sphere will start moving at t=5L2u
The third sphere will start moving at t=4Lu
The centre of mass of the system will have a final speed 2u
The centre of mass of the system will have of final speed u
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the spheres and apply the principles of conservation of momentum and the coefficient of restitution.
Step 1: Understand the Initial Setup
We have three identical spheres:
- Sphere 1 is moving towards Sphere 2 with velocity u.
- Spheres 2 and 3 are at rest.
- The distance between each pair of spheres is L.
Step 2: Collision Between Sphere 1 and Sphere 2
When Sphere 1 collides with Sphere 2, we can apply the conservation of momentum and the coefficient of restitution.
Conservation of Momentum:
Let v1 be the final velocity of Sphere 1 and v2 be the final velocity of Sphere 2 after the collision. The initial momentum is:
mu+0+0=mv1+mv2
This simplifies to:
u=v1+v2(Equation 1)
Coefficient of Restitution:
The coefficient of restitution e is given as 13. The formula is:
e=Velocity of separationVelocity of approach
Here, the velocity of approach is u and the velocity of separation is v2−v1:
13=v2−v1u
This simplifies to:
v2−v1=u3(Equation 2)
Step 3: Solve Equations 1 and 2
Now we can solve Equations 1 and 2 simultaneously.
From Equation 1:
v1=u−v2
Substituting v1 into Equation 2:
v2−(u−v2)=u3
This simplifies to:
2v2−u=u3
Multiplying through by 3 to eliminate the fraction:
6v2−3u=u
6v2=4u
v2=2u3
Substituting v2 back into Equation 1 to find v1:
u=v1+2u3
v1=u−2u3=u3
Step 4: Collision Between Sphere 2 and Sphere 3
Now Sphere 2 moves with velocity 2u3 towards Sphere 3 (which is at rest). We apply the same principles again.
Conservation of Momentum:
Let v′2 be the final velocity of Sphere 2 after the second collision and v3 be the final velocity of Sphere 3:
m2u3+0=mv′2+mv3
This simplifies to:
2u3=v′2+v3(Equation 3)
Coefficient of Restitution:
Using the same coefficient of restitution:
13=v3−v′22u3
This simplifies to:
v3−v′2=2u9(Equation 4)
Step 5: Solve Equations 3 and 4
From Equation 3:
v3=2u3−v′2
Substituting into Equation 4:
(2u3−v′2)−v′2=2u9
This simplifies to:
2u3−2v′2=2u9
Multiplying through by 9 to eliminate the fraction:
6u−18v′2=2u
4u=18v′2
v′2=2u9
Substituting v′2 back into Equation 3 to find v3:
v3=2u3−2u9
Finding a common denominator:
v3=6u9−2u9=4u9
Step 6: Calculate the Time for the Third Sphere to Start Moving
The time taken for Sphere 1 to collide with Sphere 2:
T1=Lu
The time taken for Sphere 2 to collide with Sphere 3 after Sphere 1 collides with Sphere 2:
T2=L2u3=3L2u
Total time until Sphere 3 starts moving:
T=T1+T2=Lu+3L2u=5L2u
Conclusion
The third sphere will start moving at time t=5L2u.
We have three identical spheres:
- Sphere 1 is moving towards Sphere 2 with velocity u.
- Spheres 2 and 3 are at rest.
- The distance between each pair of spheres is L.
When Sphere 1 collides with Sphere 2, we can apply the conservation of momentum and the coefficient of restitution.
Let v1 be the final velocity of Sphere 1 and v2 be the final velocity of Sphere 2 after the collision. The initial momentum is:
mu+0+0=mv1+mv2
This simplifies to:
u=v1+v2(Equation 1)
The coefficient of restitution e is given as 13. The formula is:
e=Velocity of separationVelocity of approach
Here, the velocity of approach is u and the velocity of separation is v2−v1:
13=v2−v1u
This simplifies to:
v2−v1=u3(Equation 2)
Now we can solve Equations 1 and 2 simultaneously.
v1=u−v2
v2−(u−v2)=u3
This simplifies to:
2v2−u=u3
Multiplying through by 3 to eliminate the fraction:
6v2−3u=u
6v2=4u
v2=2u3
u=v1+2u3
v1=u−2u3=u3
Now Sphere 2 moves with velocity 2u3 towards Sphere 3 (which is at rest). We apply the same principles again.
Let v′2 be the final velocity of Sphere 2 after the second collision and v3 be the final velocity of Sphere 3:
m2u3+0=mv′2+mv3
This simplifies to:
2u3=v′2+v3(Equation 3)
Using the same coefficient of restitution:
13=v3−v′22u3
This simplifies to:
v3−v′2=2u9(Equation 4)
From Equation 3:
v3=2u3−v′2
(2u3−v′2)−v′2=2u9
This simplifies to:
2u3−2v′2=2u9
Multiplying through by 9 to eliminate the fraction:
6u−18v′2=2u
4u=18v′2
v′2=2u9
v3=2u3−2u9
Finding a common denominator:
v3=6u9−2u9=4u9
The time taken for Sphere 1 to collide with Sphere 2:
T1=Lu
T2=L2u3=3L2u
T=T1+T2=Lu+3L2u=5L2u
The third sphere will start moving at time t=5L2u.
Similar Questions
A set of a identical cubical blocks lies at rest parallel to each other along a line on a smooth horizontal surface. The separation between the near surface of any two adjacent blocks is L. The block at one and is given a speed v towards the next one at time t=0. All collision are completely inelastic , then the last block starts moving at
View SolutionThe two diagrams show the situations before and after a collision between two spheres A and B of equal radii moving along the same straight line on a smooth horizontal surface. The coefficient of restitution e is
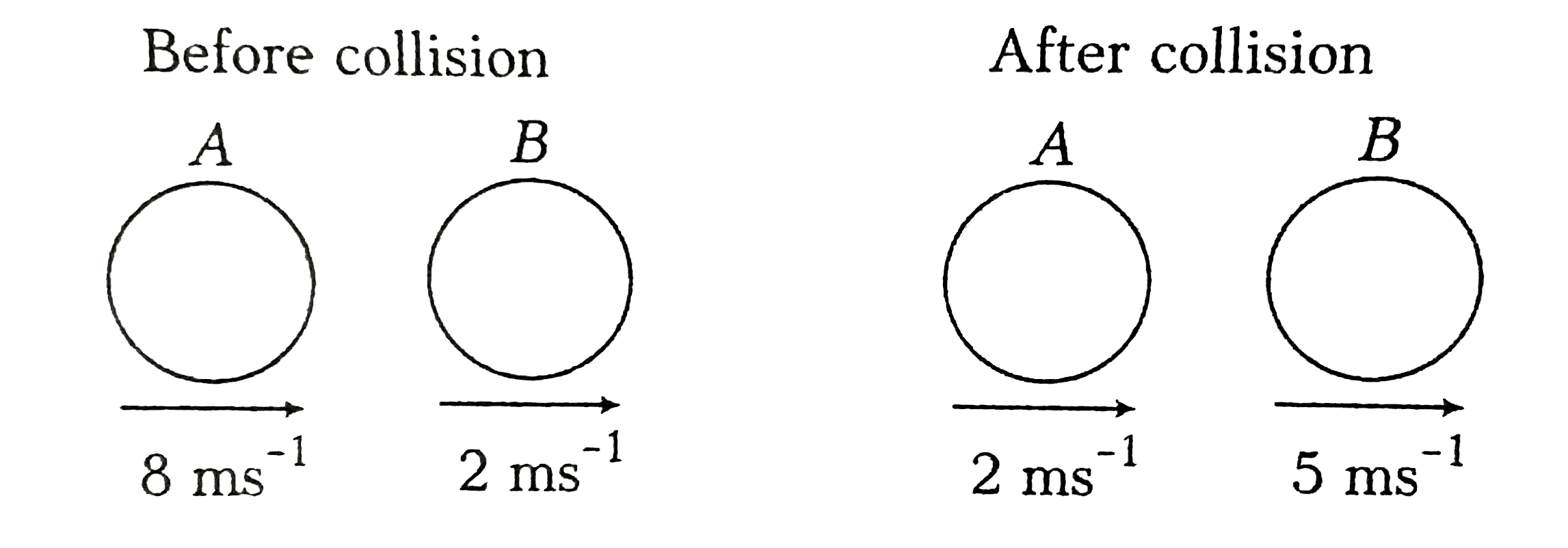
View Solution
Knowledge Check
A sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass. If e is the coefficient of restitution, then ratio of velocities of the two spheres after collision will be
A1−e1+eB1+e1−eCe+1e−1De−1e+1
Two equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
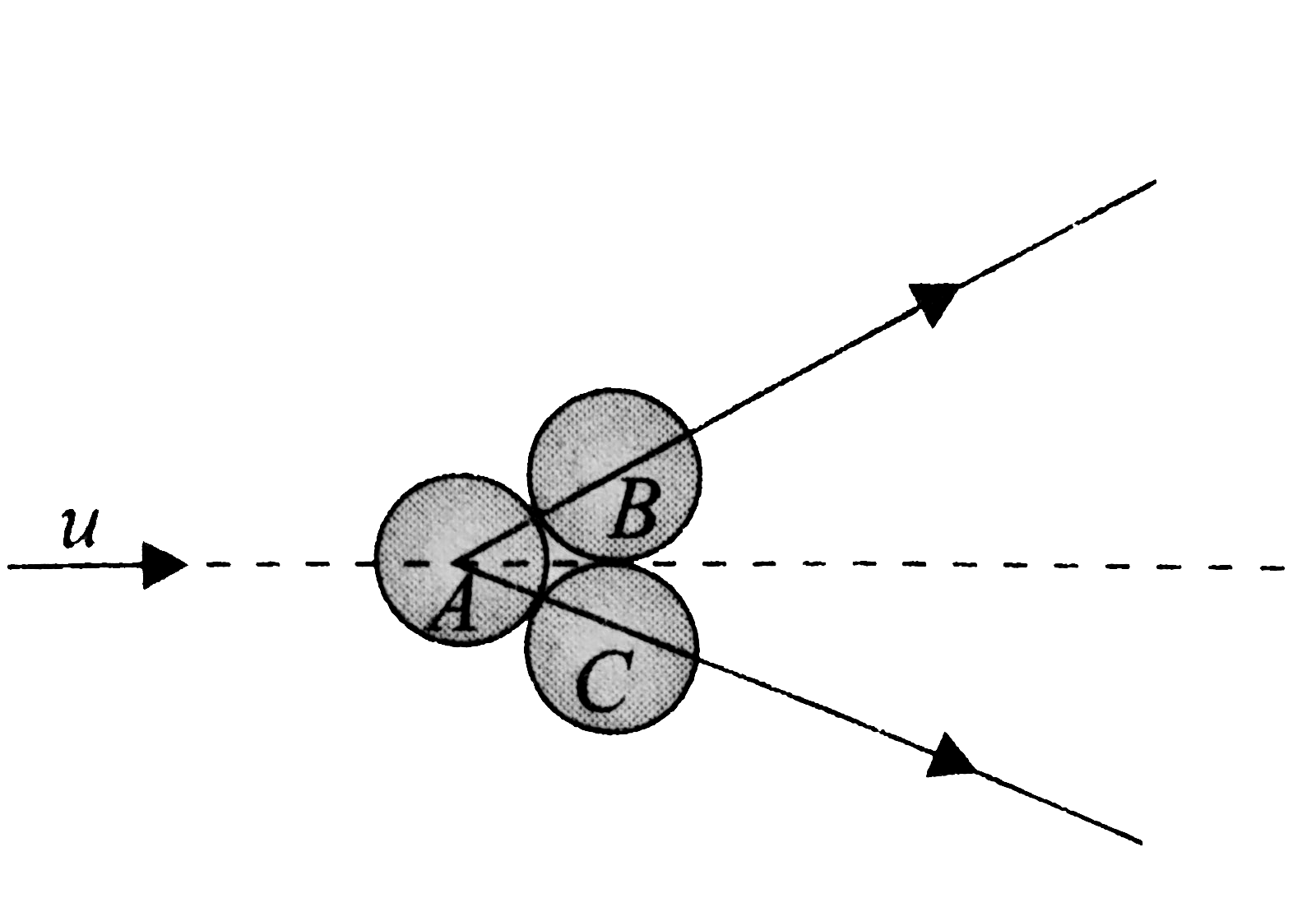
The coefficient of restitution between the two spheres A and B (or between A and C) is
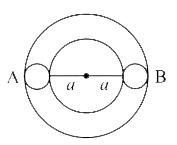
View SolutionTwo identical spheres A, B are in a smooth horizontal circular smooth groove at opposite ends of a diameter. A is projected along the groove and it impinges on B in a time interval t. Let e be the coefficient of restitution, the second impact will occur after a time
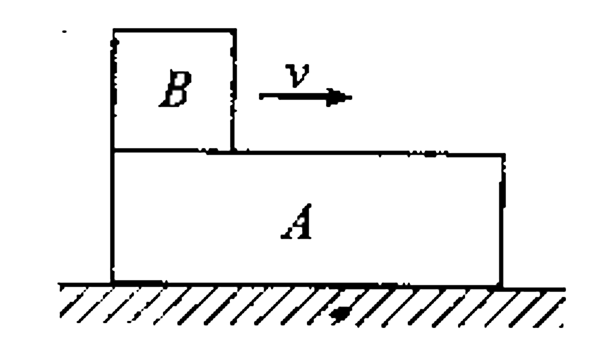
View SolutionA long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is μ:
View SolutionThree identical block A, B and C are placed on a horizontal frictionless surface. The blocks B and C are at rest but A is approaching towards B with a speed 10ms−1. The coefficient of restitution for all collisions is 0.5. The speed of the block C just after the collision is

View SolutionThree identical blocks A, B and C are placed on horizontal frictionless surface. The blocks B and C are at rest. But A is approaching towards B with a speed of 10ms−1
The coefficient of restitution for all collision is 0.5. The speed of the block C just after collision is
View Solutionn smooth identical spheres are placed in a row and their masses are in the ratio 1:3:9:_________:3n−1 . Coefficient of restitution between any two successive collisions in 1/3. If first sphere is projected with a velocity v towards the second sphere, then calculate the velocity of the last sphere after (n−1)th sphere strikes it.
View SolutionSphere A of mass m moving with a constant velocity u hits another stationary sphere B of the same mass. If e is the co-efficient of restitution, then ratio of velocities of the two spheres vA:vB after collision will be :
View Solution
