n smooth identical spheres are placed in a row and their masses are in the ratio 1:3:9:_________:3n−1 . Coefficient of restitution between any two successive collisions in 1/3. If first sphere is projected with a velocity v towards the second sphere, then calculate the velocity of the last sphere after (n−1)th sphere strikes it.
v3n
3nv
v3n−1
3n−1v
The correct Answer is:C
To solve the problem step by step, we will analyze the situation involving the smooth identical spheres and apply the principles of conservation of momentum and the coefficient of restitution.
Step 1: Understand the Mass Ratios
The masses of the spheres are given in the ratio:
- m1:m2:m3:…:mn=1:3:9:…:3n−1
We can express the masses as:
- m1=1
- m2=3
- m3=9
- mn=3n−1
Step 2: Initial Velocities
The first sphere (mass m1) is projected towards the second sphere with an initial velocity v:
- v1=v
- v2=0 (initially at rest)
Step 3: Apply Conservation of Momentum for the First Collision
Using the conservation of momentum for the collision between m1 and m2:
m1v1+m2v2=m1vf1+m2vf2
Substituting the known values:
1⋅v+3⋅0=1⋅vf1+3⋅vf2
This simplifies to:
v=vf1+3vf2(Equation 1)
Step 4: Apply Coefficient of Restitution
The coefficient of restitution e is given as 13:
e=vf2−vf1v1−v2
Substituting the values:
13=vf2−vf1v−0
This leads to:
vf2−vf1=v3(Equation 2)
Step 5: Solve Equations 1 and 2
From Equation 2:
vf2=vf1+v3
Substituting this into Equation 1:
v=vf1+3(vf1+v3)
Simplifying gives:
v=vf1+3vf1+v=4vf1+v
Thus:
0=4vf1⟹vf1=0
Then substituting back into Equation 2:
vf2=0+v3=v3
Step 6: Second Collision (m2 and m3)
Now, we consider the collision between m2 and m3:
Using conservation of momentum:
m2vf2+m3v3=m2v′f2+m3vf3
Substituting:
3⋅v3+9⋅0=3v′f2+9vf3
This simplifies to:
v=3v′f2+9vf3(Equation 3)
Step 7: Coefficient of Restitution for the Second Collision
Using the coefficient of restitution again:
13=vf3−v′f2vf2−0
This leads to:
vf3−v′f2=13⋅v3=v9(Equation 4)
Step 8: Solve Equations 3 and 4
From Equation 4:
vf3=v′f2+v9
Substituting into Equation 3:
v=3v′f2+9(v′f2+v9)
This simplifies to:
v=3v′f2+9v′f2+v=12v′f2+v
Thus:
0=12v′f2⟹v′f2=0
Then substituting back into Equation 4:
vf3=0+v9=v9
Step 9: Generalize for n Collisions
Continuing this process for n−1 collisions, we find that the velocity of the last sphere after n−1 collisions is:
vn=v3n−1
Final Answer
The velocity of the last sphere after (n−1)th collision is:
v3n−1
The masses of the spheres are given in the ratio:
- m1:m2:m3:…:mn=1:3:9:…:3n−1
- m1=1
- m2=3
- m3=9
- mn=3n−1
The first sphere (mass m1) is projected towards the second sphere with an initial velocity v:
- v1=v
- v2=0 (initially at rest)
Using the conservation of momentum for the collision between m1 and m2:
m1v1+m2v2=m1vf1+m2vf2
Substituting the known values:
1⋅v+3⋅0=1⋅vf1+3⋅vf2
This simplifies to:
v=vf1+3vf2(Equation 1)
The coefficient of restitution e is given as 13:
e=vf2−vf1v1−v2
Substituting the values:
13=vf2−vf1v−0
This leads to:
vf2−vf1=v3(Equation 2)
From Equation 2:
vf2=vf1+v3
Substituting this into Equation 1:
v=vf1+3(vf1+v3)
Simplifying gives:
v=vf1+3vf1+v=4vf1+v
Thus:
0=4vf1⟹vf1=0
Then substituting back into Equation 2:
vf2=0+v3=v3
Now, we consider the collision between m2 and m3:
Using conservation of momentum:
m2vf2+m3v3=m2v′f2+m3vf3
Substituting:
3⋅v3+9⋅0=3v′f2+9vf3
This simplifies to:
v=3v′f2+9vf3(Equation 3)
Using the coefficient of restitution again:
13=vf3−v′f2vf2−0
This leads to:
vf3−v′f2=13⋅v3=v9(Equation 4)
From Equation 4:
vf3=v′f2+v9
Substituting into Equation 3:
v=3v′f2+9(v′f2+v9)
This simplifies to:
v=3v′f2+9v′f2+v=12v′f2+v
Thus:
0=12v′f2⟹v′f2=0
Then substituting back into Equation 4:
vf3=0+v9=v9
Continuing this process for n−1 collisions, we find that the velocity of the last sphere after n−1 collisions is:
vn=v3n−1
The velocity of the last sphere after (n−1)th collision is:
v3n−1
Similar Questions
Three identical spheres lie at rest along a line on a smooth horizontal surface. The separation between any two adjacent spheres is L. The first sphere is moving with a velocity u towards the second sphere at time t = 0. The coefficient of restitution for a collision between any two blocks is 13 The correct statement is
View SolutionA sphere of mass m moving with velocity v collides head-on with another sphere of the same mass at rest. If the coefficient of resistitution e=1/2, then what is the ratio of final velocity of the second sphere to the intial velocity of the first sphere ?
View Solution
Knowledge Check
A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘If (1,-2,5) and (-3,-4, 9) are the end points of a diameter of a sphere, then the radius of the sphere is
A6 unitsB4 unitsC3 unitsD2 untis

A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling is
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
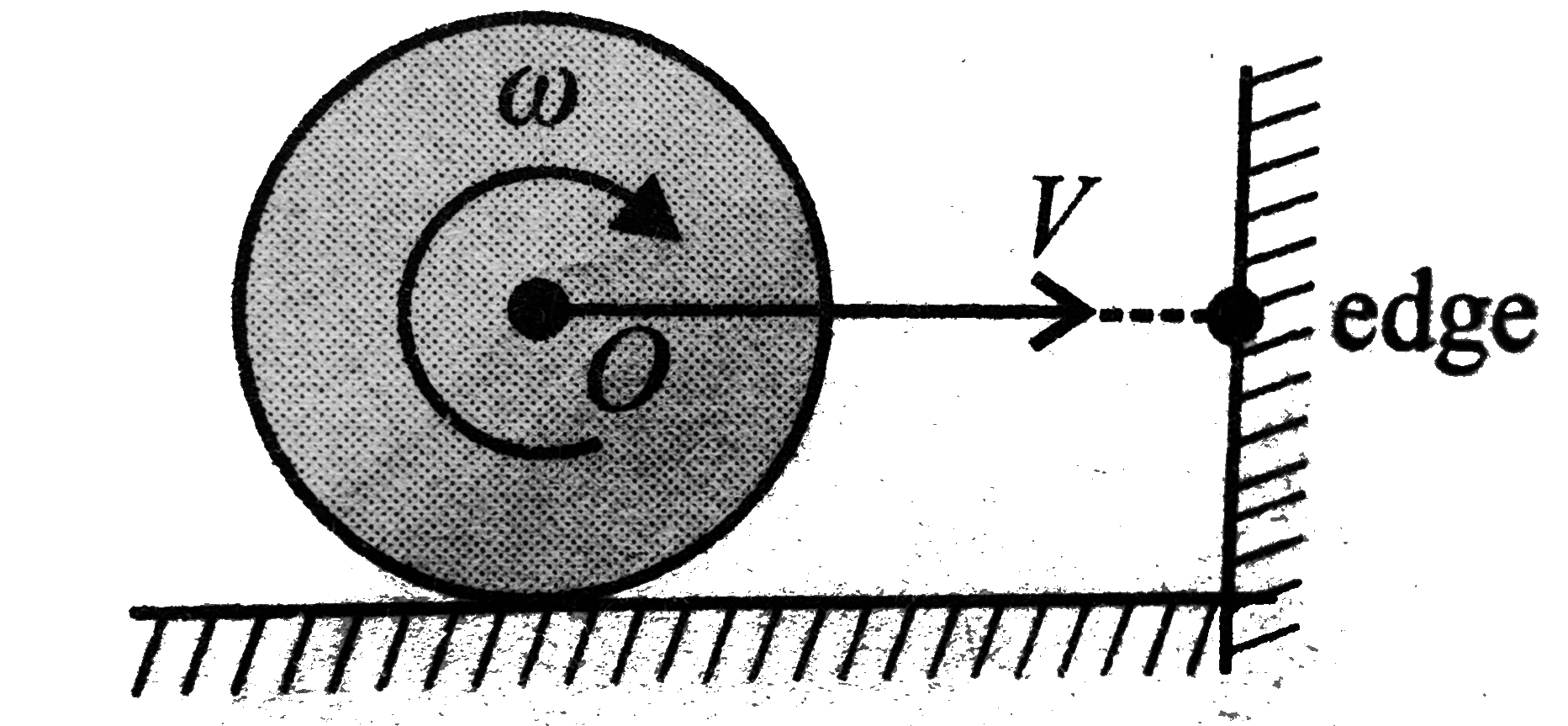
View SolutionA smooth sphere of mass m is moving on a horizontal plane with a velocity 3ˆi+ˆj when it collides with a vertical wall which is parallel to the ˆj vector. If the coefficient of restitution between the sphere and the wall is 1/2. find
a. the velocity of the sphere after impact,
b. the loss in kinetic energy caused by the impact.
c. the impulse that acts on the sphere.
View SolutionA sphere of redius R is ibn contact with a wedge. The point of contact is R5 from the ground as shown in figure.Wedge is moving with velocity 20ms−1 towards left then the velocity of the sphere at this instant will be
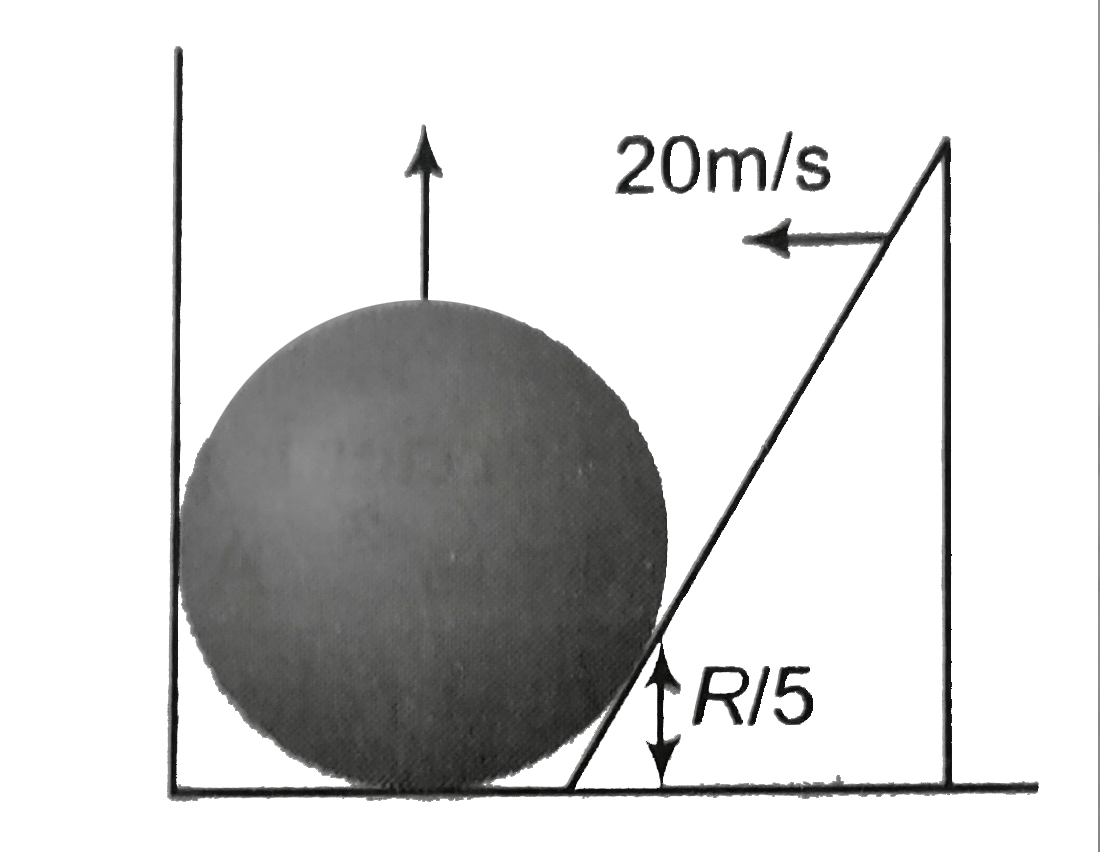
View SolutionA sphere of radius R is in contact with a wedge. The point of contact is R5 from the ground as shown in figure.Wedge is moving with velocity 20ms−1 towards left then the velocity of the sphere at this instant will be

View SolutionA smooth sphere is moving on a horizontal surface with velocity vector 3ˆi+ˆj immediately before it hits a vertical wall. The wall is parallel to the vector ˆj and the coefficient of restitution between the wall and sphere is 13. The velocity vector of the sphere after it hits the wall is :-
View Solution
