If the electric lines of force are shaped like arcs of concentric circles with their centre at point O in a certain section of an electric field , then
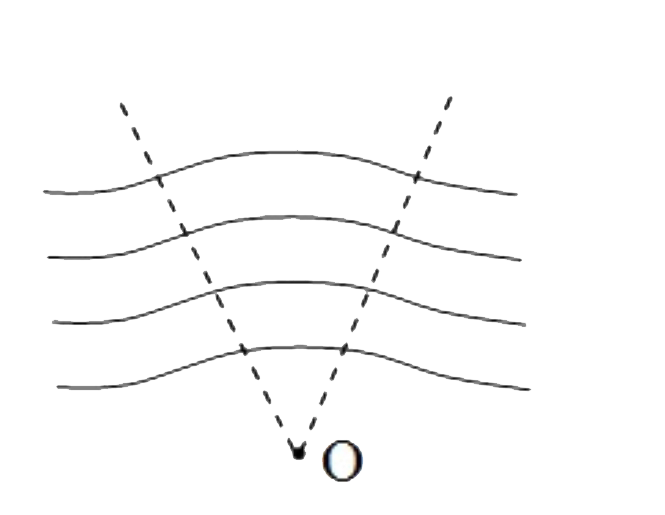
The intensity of the field in this section should at each point be inversely proportional to its distance from point O
The intensity of the field in this section should at each point be inversely proportional to square of its distance from point O
The intensity of the field in this section should at each point be inversely proportional to cube of its distance from point O
Nothing can be said
The correct Answer is:A
Step by step video & image solution for If the electric lines of force are shaped like arcs of concentric circles with their centre at point O in a certain section of an electric field , then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Show that if at some part of a field the lines of force have the from of concentric circles whose centres are at point O (as given in Fig. 3.39), the field intensity at each point in this part of the field should be inversely proportional to the distance from the point O.
 .View Solution
.View SolutionSome electric lines of force are shown in figure. For points a and B
 View Solution
View SolutionElectric lines of force about negative point charge are
View Solution(A) : No two electric lines of force can intersect each other
(R ): Tangent at any point of electric line of force gives the direction of electric field.View SolutionElectric lines of force are as shown in the figure. Then potential at point P
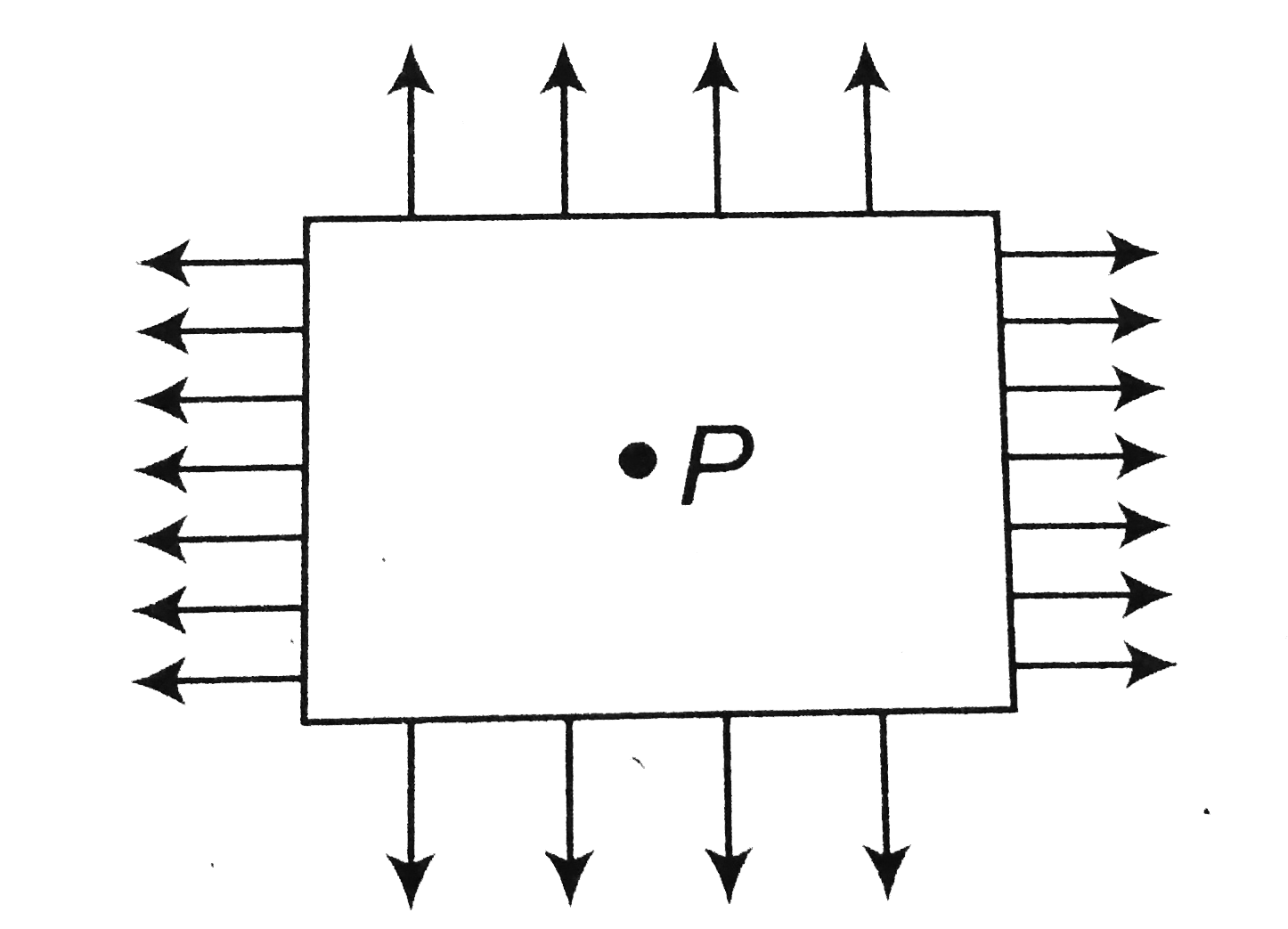 View Solution
View SolutionAssetrion: Electric lines of force never cross each other.
Reason: Electric field at a point superimpose to give one resultant electric fieldView SolutionIf electric field is uniform, then the electric lines of forces are :
View Solutionwhat is the net force on a dipole in a uniform electric field ?
View SolutionAn electron enters an electric field with its velocity in the direction of the electric lines of force. Then
View SolutionThe property of the electric line of force
(a) The tangent to the line of force at any point is parallel to the direction of .E. at that point
(b) No two lines of force intersect each otherView Solution

