Question

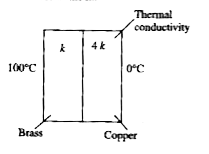
A slab consists of two parallel layers of copper and brass of the same thichness and having thermal conductivities in the ratio $1:4$ If the free face of brass is at ${100}^{\circ }C$ anf that of copper at $0^{\circ }C$ the temperature of interface is .

Options

A. (a)`80^@C`
B. (b)`20^@C`
C. (c)`60^@C`
D. (d)`40^@C`

Answer

A

Explanation

To solve the problem step by step, we will use the concept of thermal conduction through two layers of materials with different thermal conductivities.

1. Identify the Given Data:
- Thermal conductivity of copper (K_c) = 1K
- Thermal conductivity of brass (K_b) = 4K
- Temperature of brass face (T_b) = 100°C
- Temperature of copper face (T_c) = 0°C
- Let the thickness of each layer be 'd'.

2. Set Up the Temperature Gradient:
- Let the temperature at the interface between the two materials be θ (in °C).
- The temperature difference across the brass layer is (T_b - θ) = (100 - θ)°C.
- The temperature difference across the copper layer is (θ - T_c) = (θ - 0)°C = θ°C.

3. Apply the Heat Conduction Equation:
- According to Fourier's law of heat conduction, the heat flow (Q) through each layer must be equal since they are in steady state.
- For brass:
\( Q = \frac{K_b \cdot A \cdot (T_b - \theta)}{d} = \frac{4K \cdot A \cdot (100 - \theta)}{d} \)
- For copper:
\( Q = \frac{K_c \cdot A \cdot (\theta - T_c)}{d} = \frac{1K \cdot A \cdot \theta}{d} \)

4. Equate the Heat Flow:
- Since both expressions for Q are equal:
\( \frac{4K \cdot A \cdot (100 - \theta)}{d} = \frac{1K \cdot A \cdot \theta}{d} \)
- The area (A) and thickness (d) cancel out, leading to:
\( 4(100 - \theta) = \theta \)

5. Solve for θ:
- Expanding the equation:
\( 400 - 4\theta = \theta \)
- Rearranging gives:
\( 400 = 5\theta \)
- Therefore, solving for θ:
\( \theta = \frac{400}{5} = 80°C \)

6. Conclusion:
- The temperature at the interface is θ = 80°C.