A slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
K1 + K2
K1 + K2/2
2K1 + K2 /K1 + k2
K1 + K2/2KK2
The correct Answer is:B
To find the equivalent thermal conductivity of a slab consisting of two layers of different materials with the same thickness, we can follow these steps:
1. Identify the Parameters:
- Let the thermal conductivities of the two materials be K1 and K2.
- Let the thickness of each layer be L.
- Let the cross-sectional area of each layer be A.
2. Determine the Thermal Resistances:
- The thermal resistance R1 for the first layer is given by:
R1=LK1⋅A
- The thermal resistance R2 for the second layer is given by:
R2=LK2⋅A
3. Calculate the Equivalent Resistance:
- Since the two layers are in parallel, the equivalent thermal resistance Req can be calculated using the formula:
1Req=1R1+1R2
- Substituting the expressions for R1 and R2:
1Req=K1⋅AL+K2⋅AL
4. Simplify the Equation:
- Factor out common terms:
1Req=AL(K1+K2)
- Therefore, we can express Req as:
Req=LA(K1+K2)
5. Relate Equivalent Resistance to Equivalent Conductivity:
- The equivalent thermal resistance can also be expressed in terms of the equivalent thermal conductivity Keq:
Req=LKeq⋅(2A)
- Here, 2A is used because the total area for the parallel combination is twice the area of one layer.
6. Set the Two Expressions for Req Equal:
- Equating the two expressions for Req:
LA(K1+K2)=LKeq⋅(2A)
7. Solve for Keq:
- Cancel L and A from both sides:
1K1+K2=12Keq
- Rearranging gives:
2Keq=K1+K2
- Thus, the equivalent thermal conductivity is:
Keq=K1+K22
Final Answer:
The equivalent thermal conductivity of the slab is:
Keq=K1+K22
- Let the thermal conductivities of the two materials be K1 and K2.
- Let the thickness of each layer be L.
- Let the cross-sectional area of each layer be A.
- The thermal resistance R1 for the first layer is given by:
R1=LK1⋅A
- The thermal resistance R2 for the second layer is given by:
R2=LK2⋅A
- Since the two layers are in parallel, the equivalent thermal resistance Req can be calculated using the formula:
1Req=1R1+1R2
- Substituting the expressions for R1 and R2:
1Req=K1⋅AL+K2⋅AL
- Factor out common terms:
1Req=AL(K1+K2)
- Therefore, we can express Req as:
Req=LA(K1+K2)
- The equivalent thermal resistance can also be expressed in terms of the equivalent thermal conductivity Keq:
Req=LKeq⋅(2A)
- Here, 2A is used because the total area for the parallel combination is twice the area of one layer.
- Equating the two expressions for Req:
LA(K1+K2)=LKeq⋅(2A)
- Cancel L and A from both sides:
1K1+K2=12Keq
- Rearranging gives:
2Keq=K1+K2
- Thus, the equivalent thermal conductivity is:
Keq=K1+K22
The equivalent thermal conductivity of the slab is:
Keq=K1+K22
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.4
29 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Taking it together
51 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionA composite slab is made of two parallel layers of two different materials of thermal conductivities K1andK2 are of same thickness. Show that the equivalent thermal conductivity of the slab is 2K1K2K1+K2
View Solution
Knowledge Check
Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
A23KB√2KC3KD43KThe slab shown in the figure consists of two parallel layers of cooper anb brass of same thickness and having thermal conductivites in the ratio 4:1. IF the free face of the brass is at 100∘C and that of copper is at 0∘C, then the temperature of the interface will be
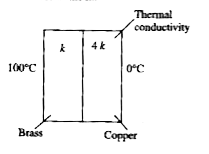 A20∘CB30∘CC40∘CD25∘C
A20∘CB30∘CC40∘CD25∘CIn the question number of 45, the equivalent thermal conductivity of the compound bar is
AK1K2K1+K2B2K1K2K1+K2CK1K1+K2DK2K1+K2
Three rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionA slab consists of two parallel layers of copper and brass of the same thichness and having thermal conductivities in the ratio 1:4 If the free face of brass is at 100∘C anf that of copper at 0∘C the temperature of interface is .
View SolutionA composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivities K1 and K2 . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View Solution
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution