A simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
12mgl
12mglcosθ
mgl(1−cosθ)
12mglsinθ
The correct Answer is:C
To find the maximum kinetic energy of a bob of mass m in a simple pendulum of length l with a maximum angular displacement θ, we can follow these steps:
1. Understand the Pendulum's Motion:
- A simple pendulum swings back and forth. The maximum angular displacement is denoted as θ. At the extreme positions, the pendulum has maximum potential energy and zero kinetic energy.
2. Identify the Positions:
- At the extreme position (maximum displacement), the bob is momentarily at rest, so the kinetic energy (KE) is zero, and the potential energy (PE) is at its maximum.
- At the mean position (the lowest point of the swing), the kinetic energy is maximum, and the potential energy is zero.
3. Calculate the Height (h):
- The height h of the bob at the extreme position can be calculated using trigonometry. If we consider the vertical line from the pivot to the lowest point of the swing:
- The length of the pendulum is l.
- The vertical distance from the pivot to the bob at the extreme position is l⋅cos(θ).
- Therefore, the height h from the lowest point to the extreme position is:
\(
h = l - l \cos(\theta) = l(1 - \cos(\theta))
\)
4. Calculate the Potential Energy (PE):
- The potential energy at the extreme position is given by:
\(
PE = mgh = mg \cdot h = mg \cdot l(1 - \cos(\theta)) = mgl(1 - \cos(\theta))
\)
5. Apply Conservation of Energy:
- Since energy is conserved in the absence of friction, the total mechanical energy at the extreme position (which is all potential energy) is equal to the total mechanical energy at the mean position (which is all kinetic energy).
- Therefore, we have:
\(
KE_{\text{max}} = PE_{\text{max}} = mgl(1 - \cos(\theta))
\)
6. Conclusion:
- The maximum kinetic energy of the bob is:
\(
KE_{\text{max}} = mgl(1 - \cos(\theta))
\)
Final Answer:
The maximum kinetic energy of the bob of mass m is:
\(
KE_{\text{max}} = mgl(1 - \cos(\theta))
\)
- A simple pendulum swings back and forth. The maximum angular displacement is denoted as θ. At the extreme positions, the pendulum has maximum potential energy and zero kinetic energy.
- At the extreme position (maximum displacement), the bob is momentarily at rest, so the kinetic energy (KE) is zero, and the potential energy (PE) is at its maximum.
- At the mean position (the lowest point of the swing), the kinetic energy is maximum, and the potential energy is zero.
- The height h of the bob at the extreme position can be calculated using trigonometry. If we consider the vertical line from the pivot to the lowest point of the swing:
- The length of the pendulum is l.
- The vertical distance from the pivot to the bob at the extreme position is l⋅cos(θ).
- Therefore, the height h from the lowest point to the extreme position is:
\(
h = l - l \cos(\theta) = l(1 - \cos(\theta))
\)
- The potential energy at the extreme position is given by:
\(
PE = mgh = mg \cdot h = mg \cdot l(1 - \cos(\theta)) = mgl(1 - \cos(\theta))
\)
- Since energy is conserved in the absence of friction, the total mechanical energy at the extreme position (which is all potential energy) is equal to the total mechanical energy at the mean position (which is all kinetic energy).
- Therefore, we have:
\(
KE_{\text{max}} = PE_{\text{max}} = mgl(1 - \cos(\theta))
\)
- The maximum kinetic energy of the bob is:
\(
KE_{\text{max}} = mgl(1 - \cos(\theta))
\)
The maximum kinetic energy of the bob of mass m is:
\(
KE_{\text{max}} = mgl(1 - \cos(\theta))
\)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective13videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct18videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Assertion And Reason28videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
Assertion: The motion of a simple pendulum is simple harmoni for all angular displacement.
Reason: Motion of simple pendulum is independent of the angular displacement.AIf both assertion and reson are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
The bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionA simple pendulum of length l and bob of mass m is displaced from its equilibrium position O to a position P so that hight of P above O is h . If is then released. What is the tension in the string when the bob passes through the through the equilibrium position O ? Neglect friction. v is the velocity of the bob at O
View SolutionA pendulum has maximum kinetic energy K1 If its length is doubled keeping amplitude same then maximum kinetic energy becomes K2 .Then relation between K1andK2 is
View SolutionA simple pendulum is oscillating with angular displacement 90∘ For what angle with vertical the acceleration of bob direction horizontal?
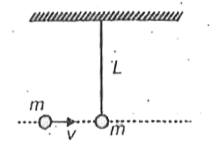
View SolutionA small ball of mass m moving with speed v (>√2gL) undergoes an elastic head on collision with a stationary bon of identical mass of a simple pendulum of length L. The maximum height h, from the equilibrium position, to which the bob rises after collision is
 View Solution
View SolutionA simple pendulum is oscillating without damiping, When the displacement of the bob is less than maximum, its acceleration vector →a is correctly show in:
View SolutionA simple pendulum of length 1 oscillates aboμt the mean position as shown in the figure. If the total energy of the pendulum is E, the velocity of the pendulum bob of mass m at point P is:
 View Solution
View Solution

