Two particles of mass m and 2m have their position vectors as a function of time as respectively (where t is the time). Which one of the following graphs represents the path of the centre of mass ?
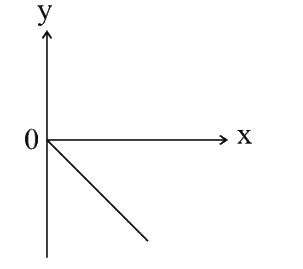
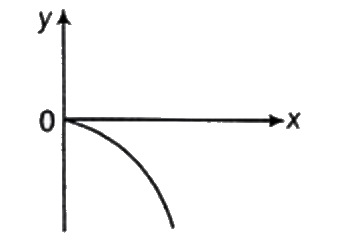
The correct Answer is:D
To find the path of the center of mass of the two particles with given position vectors, we can follow these steps:
Step 1: Identify the position vectors
The position vectors of the two particles are given as:
- For particle 1 (mass m):
r1(t)=^i−t3^j+2t2^k
- For particle 2 (mass 2m):
r2(t)=t^i−t3^j−t2^k
Step 2: Write the formula for the center of mass
The position vector of the center of mass rcom is given by:
rcom=m1r1+m2r2m1+m2
where m1=m and m2=2m.
Step 3: Substitute the values into the formula
Substituting the values of m1, m2, r1, and r2:
rcom=mr1+2mr2m+2m
This simplifies to:
rcom=m(^i−t3^j+2t2^k)+2m(t^i−t3^j−t2^k)3m
Step 4: Simplify the expression
Now, we can simplify the numerator:
=m^i−mt3^j+2m⋅2t2^k+2mt^i−2mt3^j−2mt2^k3m
Combining like terms:
=(m+2mt)^i+(−mt3−2mt3)^j+(2mt2−2mt2)^k3m
This simplifies to:
=(1+2t)^i−3t3^j3
Step 5: Write the components of the center of mass
From the above expression, we can identify the components:
- x=1+2t3
- y=−t3
Step 6: Analyze the path
To analyze the path, we can express y in terms of x:
From x=1+2t3, we can express t as:
t=3x−12
Substituting this into the equation for y:
y=−(3x−12)3
This indicates that the path is a cubic curve in the fourth quadrant since y will be negative for positive x.
Conclusion
The graph representing the path of the center of mass is a curve in the fourth quadrant, which corresponds to option D.
---
The position vectors of the two particles are given as:
- For particle 1 (mass m):
r1(t)=^i−t3^j+2t2^k
- For particle 2 (mass 2m):
r2(t)=t^i−t3^j−t2^k
The position vector of the center of mass rcom is given by:
rcom=m1r1+m2r2m1+m2
where m1=m and m2=2m.
Substituting the values of m1, m2, r1, and r2:
rcom=mr1+2mr2m+2m
This simplifies to:
rcom=m(^i−t3^j+2t2^k)+2m(t^i−t3^j−t2^k)3m
Now, we can simplify the numerator:
=m^i−mt3^j+2m⋅2t2^k+2mt^i−2mt3^j−2mt2^k3m
Combining like terms:
=(m+2mt)^i+(−mt3−2mt3)^j+(2mt2−2mt2)^k3m
This simplifies to:
=(1+2t)^i−3t3^j3
From the above expression, we can identify the components:
- x=1+2t3
- y=−t3
To analyze the path, we can express y in terms of x:
From x=1+2t3, we can express t as:
t=3x−12
Substituting this into the equation for y:
y=−(3x−12)3
This indicates that the path is a cubic curve in the fourth quadrant since y will be negative for positive x.
The graph representing the path of the center of mass is a curve in the fourth quadrant, which corresponds to option D.
Similar Questions
The position vectors of three particles of mass m1=1kg,m2=2kgandm3=3kg are r1=((ˆi+4ˆj+ˆk)m, r2=((ˆi+(ˆj+ˆk)m and r3=(2ˆi−(ˆj−(ˆ2k)m, respectively. Find the position vector of their center of mass.
View SolutionProve that lines →r=(ˆi+ˆj+ˆk)+t(ˆi−ˆj+ˆk)and→r=(3ˆi−ˆk)+s(4ˆj−16ˆk) intersect. Also find the position vector of their point of intersection
View SolutionFind the shortest distance between the lines whose vector equations are→r=(1−t)ˆi+(t−2)ˆj+(3−2t)ˆkand →r=(s+1)ˆi+(2s−1)ˆj−(2s+1)ˆk
View SolutionFind the Cartesian form the equation of the plane →r=(s−2t)ˆi+(3−t)ˆj+(2s+t)ˆk.
View SolutionFind the image of the point having position vector ˆi+3ˆj+4ˆk in the plane →r.(2ˆi−ˆj+ˆk)+3=0
View SolutionFind the value of λ, if the points with position vectors 3ˆi−2ˆj−ˆk,2ˆi+3ˆj−4ˆk,−ˆi+ˆj+2ˆk,4ˆi+5ˆj+λˆk are coplanar.
View SolutionA particle is moving with a position vector, →r=[a0sin(2πt)ˆi+a0cos(2πt)ˆj]. Then -
View SolutionA particle move in x−y plane such that its position vector varies with time as →r=(2sin3t)ˆj+2(1−cos3t)ˆj. Find the equation of the trajectory of the particle.
View SolutionProve that the following vectors are coplanar: ˆi+ˆj+ˆk, 2ˆi+3ˆj−ˆk and−ˆi−2ˆj+2ˆk
View SolutionThe position vector of a particle →R as a funtion of time is given by:
→R=4sin(2πt)ˆi+4cos(2πt)ˆj
Where R is in meters, t is in seconds and ˆi and ˆj denote until vectors along x-and y- directions, respectively Which one of the following statements is wrong for the motion of particle ?
View Solution
