A steady current is set up in a metalic wire of non- uniform cross-section. How is the rate of flow free electrons related
R∝A−1
R∝A
R∝A2
R is independent of A
The correct Answer is:A
To solve the question regarding the relationship between the rate of flow of free electrons and the cross-sectional area of a metallic wire with a non-uniform cross-section, we can follow these steps:
1. Understanding Current:
- The rate of flow of free electrons in a conductor is defined as the electric current (I). Current is the amount of charge (Q) passing through a cross-section of the wire per unit time (t).
- Mathematically, I=Qt.
2. Current Density:
- Current density (J) is defined as the current per unit area of cross-section. It can be expressed as:
J=IA
where A is the cross-sectional area.
3. Drift Velocity:
- The drift velocity (v_d) of free electrons is related to current density and charge density (n) as follows:
J=nevd
where e is the charge of an electron.
4. Relation to Cross-Sectional Area:
- From the equations above, we can see that if the area A changes, the current density J and drift velocity vd will also change. Specifically, if the area decreases, the current density increases, assuming the current remains constant.
5. Independence of Current:
- The total current I remains constant regardless of the cross-sectional area of the wire. This means that while J and vd are dependent on the area, the total current I is independent of the area.
6. Conclusion:
- Therefore, the rate of flow of free electrons (current) is independent of the area of cross-section in a metallic wire with a steady current.
Final Answer:
The rate of flow of free electrons (current) is independent of the cross-sectional area of the wire.
---
- The rate of flow of free electrons in a conductor is defined as the electric current (I). Current is the amount of charge (Q) passing through a cross-section of the wire per unit time (t).
- Mathematically, I=Qt.
- Current density (J) is defined as the current per unit area of cross-section. It can be expressed as:
J=IA
where A is the cross-sectional area.
- The drift velocity (v_d) of free electrons is related to current density and charge density (n) as follows:
J=nevd
where e is the charge of an electron.
- From the equations above, we can see that if the area A changes, the current density J and drift velocity vd will also change. Specifically, if the area decreases, the current density increases, assuming the current remains constant.
- The total current I remains constant regardless of the cross-sectional area of the wire. This means that while J and vd are dependent on the area, the total current I is independent of the area.
- Therefore, the rate of flow of free electrons (current) is independent of the area of cross-section in a metallic wire with a steady current.
The rate of flow of free electrons (current) is independent of the cross-sectional area of the wire.
Similar Questions
a. A steady current flows in a metallic conductor of non - uniform cross section. State which of the quantities i.e., current density, electric field, and drift velocity remain constant?
b. A steady current passes through a cylindrical conductor. Is there an electorn field inside the conductor?
View SolutionWhen a steady current flows through a metal conductor of non-uniform cross-section , then drift velocity is
View SolutionA Steady current flows in a metalic conductor of non uniform cross section. The quantity/quantities which remain constant along the length of the conductor is/are
View SolutionA : When a steady current flows through a conductor of non - uniform cross-section , the current density , electric field and drift velcoity do not remain constant.
R : For a constant current the current density electric field and drift velocity are inversely proportional to cross - sectional area.
View SolutionA stready current i is flowing through a conductor of uniform cross-section. Any segment of the conductor has
View SolutionAssertion : If a current flows through a wire of non-uniform cross-section, potential difference per unit length of wire is same throughout the length of wire.
Reason : Current through the wire is same at all cross-sections.
View Solution
Assertion : Current I is flowing through a cylindrical wire of non-uniform cross-section as shown. Section of wire near A will be more heated compared to the section near B.
Reason : Current density near A is more.
View SolutionThere is a current of 40 ampere in a wire of 10−6m2 are of cross-section. If the number of free electron per m3 is 1029 then the drift velocity will be
View SolutionA current passes through a wire of nonuniform cross-section. Which of the following quantites are independent of the cross section?
View SolutionCurrent is flowing through a wire of non-uniform cross section. Cross section of wire at A is les than the cross section of wire at B. Then match the following
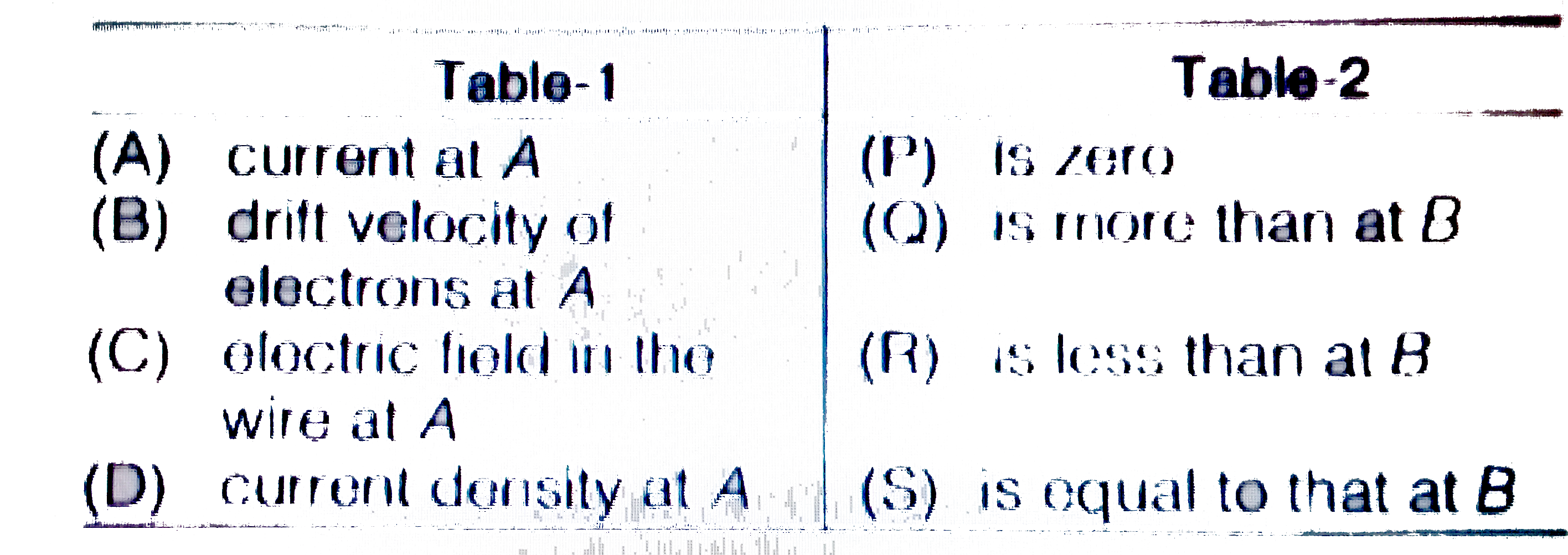
View Solution
