A stready current i is flowing through a conductor of uniform cross-section. Any segment of the conductor has
zero charge
only positive charge
only negative charge
charge proportional to current i
The correct Answer is:A
To solve the problem, we need to analyze the behavior of charge in a conductor through which a steady current I is flowing. Here’s a step-by-step solution:
Step 1: Understanding Current
Current (I) is defined as the rate of flow of charge. Mathematically, it is given by:
I=dQdt
where dQ is the amount of charge flowing through a cross-section of the conductor in a small time interval dt.
Hint: Remember that current is the flow of charge per unit time.
Step 2: Charge Flow in a Conductor
In a steady state, the current flowing into any segment of the conductor must equal the current flowing out of that segment. This means:
Iin=Iout=I
Hint: Think about the conservation of charge – what goes in must come out in a steady current.
Step 3: Analyzing Charge in a Segment
Let’s consider a small segment of the conductor. If we denote the charge entering the segment as Qin and the charge leaving as Qout, we can express these charges in terms of current:
Qin=I⋅tandQout=I⋅t
for a time duration t.
Hint: Relate the charge to the current using the time duration for which the current flows.
Step 4: Net Charge in the Segment
The net charge (Qnet) in the segment can be calculated as:
Qnet=Qout−Qin=(I⋅t)−(I⋅t)=0
Hint: Consider what happens when you subtract equal quantities.
Step 5: Conclusion
Since the net charge in any segment of the conductor is zero, we conclude that:
- Any segment of the conductor has no excess charge at any moment.
Final Answer: The net charge in any segment of the conductor is zero.
Current (I) is defined as the rate of flow of charge. Mathematically, it is given by:
I=dQdt
where dQ is the amount of charge flowing through a cross-section of the conductor in a small time interval dt.
In a steady state, the current flowing into any segment of the conductor must equal the current flowing out of that segment. This means:
Iin=Iout=I
Let’s consider a small segment of the conductor. If we denote the charge entering the segment as Qin and the charge leaving as Qout, we can express these charges in terms of current:
Qin=I⋅tandQout=I⋅t
for a time duration t.
The net charge (Qnet) in the segment can be calculated as:
Qnet=Qout−Qin=(I⋅t)−(I⋅t)=0
Since the net charge in any segment of the conductor is zero, we conclude that:
- Any segment of the conductor has no excess charge at any moment.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
When a steady current flows through a metal conductor of non-uniform cross-section , then drift velocity is
View SolutionWhen no current is passed through a conductor,
View SolutionA : When a steady current flows through a conductor of non - uniform cross-section , the current density , electric field and drift velcoity do not remain constant.
R : For a constant current the current density electric field and drift velocity are inversely proportional to cross - sectional area.
View SolutionAssertion : If a current is flowing through a conducting wire of non-uniform cross-section, drift speed and resistance both will increase at a section where cross-sectional area is less.
Reason : Current density at such sections is more where cross-sectional area is less.
View Solutiona. A steady current flows in a metallic conductor of non - uniform cross section. State which of the quantities i.e., current density, electric field, and drift velocity remain constant?
b. A steady current passes through a cylindrical conductor. Is there an electorn field inside the conductor?
View SolutionWhen a current passes through a resistor, its temperature increases. Is it an adiabatic process?
View SolutionA steady electric current is flowing through a cylindrical conductor. Then,
View Solution
Assertion : Current I is flowing through a cylindrical wire of non-uniform cross-section as shown. Section of wire near A will be more heated compared to the section near B.
Reason : Current density near A is more.
View SolutionA Steady current flows in a metalic conductor of non uniform cross section. The quantity/quantities which remain constant along the length of the conductor is/are
View SolutionCurrent is flowing through a wire of non-uniform cross section. Cross section of wire at A is les than the cross section of wire at B. Then match the following
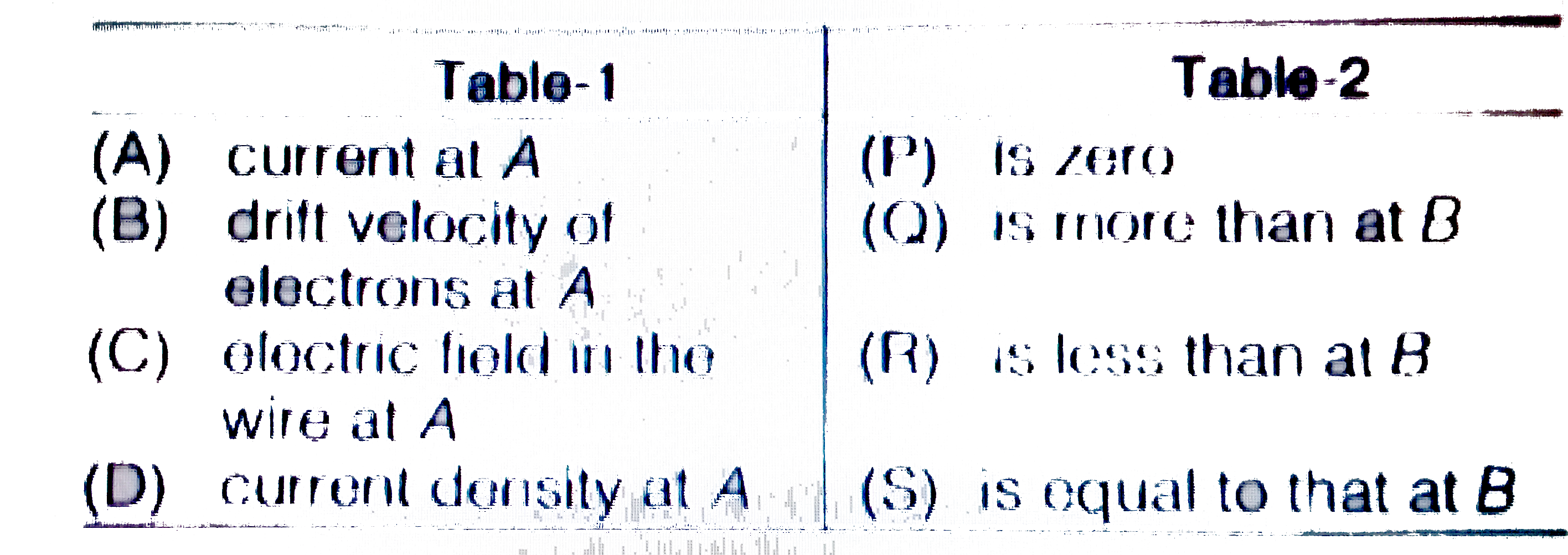
View Solution
