Young's modulus of elasticity is the ratio of
Hydraulic stress and hydraulic strain
Shearing stress and shearing strain
Tensile stress and longitudinal strain
Bulk stress and longitudinal strain
The correct Answer is:C
To solve the question regarding Young's modulus of elasticity, we need to understand the definitions and relationships between stress, strain, and the different types of moduli.
1. Understanding Young's Modulus:
- Young's modulus (E) is a measure of the stiffness of a solid material. It quantifies the relationship between stress (force per unit area) and strain (deformation) in a material in the linear elastic region of the stress-strain curve.
2. Defining Stress and Strain:
- Stress is defined as the force (F) applied per unit area (A):
Stress=FA
- Strain is defined as the change in length (ΔL) divided by the original length (L):
Strain=ΔLL
3. Relationship of Young's Modulus:
- Young's modulus is defined mathematically as:
E=Tensile StressLongitudinal Strain=FAΔLL
4. Identifying the Correct Ratio:
- From the definition, we can see that Young's modulus is specifically the ratio of tensile stress to longitudinal strain.
- Therefore, the correct answer to the question is that Young's modulus of elasticity is the ratio of tensile stress to longitudinal strain.
5. Eliminating Incorrect Options:
- The other options mentioned (hydraulic stress and strain, shearing stress and strain, bulk stress and strain) do not relate to Young's modulus:
- Hydraulic stress and strain relate to fluids.
- Shearing stress and strain relate to the modulus of rigidity (shear modulus).
- Bulk stress and strain relate to the bulk modulus.
Conclusion:
Thus, the correct answer is that Young's modulus of elasticity is the ratio of tensile stress to longitudinal strain.
- Young's modulus (E) is a measure of the stiffness of a solid material. It quantifies the relationship between stress (force per unit area) and strain (deformation) in a material in the linear elastic region of the stress-strain curve.
- Stress is defined as the force (F) applied per unit area (A):
Stress=FA
- Strain is defined as the change in length (ΔL) divided by the original length (L):
Strain=ΔLL
- Young's modulus is defined mathematically as:
E=Tensile StressLongitudinal Strain=FAΔLL
- From the definition, we can see that Young's modulus is specifically the ratio of tensile stress to longitudinal strain.
- Therefore, the correct answer to the question is that Young's modulus of elasticity is the ratio of tensile stress to longitudinal strain.
- The other options mentioned (hydraulic stress and strain, shearing stress and strain, bulk stress and strain) do not relate to Young's modulus:
- Hydraulic stress and strain relate to fluids.
- Shearing stress and strain relate to the modulus of rigidity (shear modulus).
- Bulk stress and strain relate to the bulk modulus.
Thus, the correct answer is that Young's modulus of elasticity is the ratio of tensile stress to longitudinal strain.
Similar Questions
A bar of mass m and length l is hanging from point A as shown in the figure . If the Young's modulus of elasticity of the bar is Y and area of cross - section of the wire is A, then the increase in its length due to its own weight will be

View SolutionAssertion Young's modulus of elasticity is not defined for liquids.
Reason Liquids cannot be stretched as wires.
View SolutionIn Searl's experiment, which is used to find Young's Modulus of elasticity, the diameter of experimental wire is D=0.05cm (measured by a scale of least count 0.001cm) and length is L=110cm (measured by a scale of least count 0.1cm). A weight of 50N causes an extension of X=0.125cm (measured by a micrometer of least count 0.001cm). find the maximum possible error in the values of Young's modulus. Screw gauge and meter scale are free error.
View SolutionAssertion If length of a wire is halved, its Young's modulus of elasticity will become two times.
Reason The ratio of longitudinal stress and longitudinal strain is called Young's modulus of elasticity.
View SolutionStress-strain curve for four metals are shown in figure. The maximum Young's modulus of elasticity is for metal

View SolutionA metallic wire is stretched by suspending a weight of it. If α is the longitudinal strain and Y is its Young's modulus of elasticity, then slow that the elastic potential energy per unit volume is given by 12Yα2.
View SolutionFor the experimental determination of Young.s modulus of elasticity Y of the material of a given wire by using Searle.s apparatus, the spherometer reading while load increasing and decreasing are tabulated below:
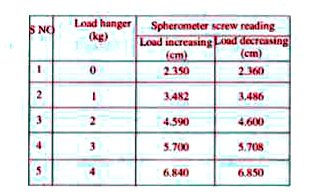
The mean extension for 2kg load is
View SolutionA structural steel rod has a radius r =10mm and a length l.=1m When a force F=100kN is applied, it stretches it along its length. Young's modulus of elasticity of the structural steel is 2.0×1011Nm−2. What is the elastic energy density of the steel rod ?
View SolutionA structural steel rod has a radius r(=10 mm) and a length l(=1 m). When a force F(= 100 kN) is applied, it stretches it along its length. Young's modulus of elasticity of the structural steel is 2.0×104Nm−2. What is the elastic energy density of the steel rod ?
View Solutionisobaric modulus of elasticity is
View Solution
