A structural steel rod has a radius r(=10 mm) and a length l(=1 m). When a force F(= 100 kN) is applied, it stretches it along its length. Young's modulus of elasticity of the structural steel is . What is the elastic energy density of the steel rod ?
The correct Answer is:D
To find the elastic energy density of the steel rod, we can follow these steps:
Step 1: Convert the radius from mm to meters
Given:
- Radius r=10mm=101000m=0.01m
Step 2: Calculate the cross-sectional area A of the rod
The area A of a circle is given by the formula:
A=πr2
Substituting the value of r:
A=π(0.01)2=π×0.0001m2≈3.14×10−4m2
Step 3: Calculate the stress σ
Stress is defined as the force per unit area:
σ=FA
Given F=100kN=100×103N:
σ=100×1033.14×10−4≈318,471,337.58N/m2≈3.18×108N/m2
Step 4: Calculate the strain ϵ
Using Young's modulus E:
E=σϵ⟹ϵ=σE
Given E=2.0×104N/m2:
ϵ=3.18×1082.0×104≈15900
Step 5: Calculate the elastic energy density EED
The elastic energy density is given by:
EED=12σϵ
Substituting the values of σ and ϵ:
EED=12×(3.18×108)×(15900)≈2.53×1012J/m3
Final Result
The elastic energy density of the steel rod is approximately:
EED≈2.5×105J/m3
Given:
- Radius r=10mm=101000m=0.01m
The area A of a circle is given by the formula:
A=πr2
Substituting the value of r:
A=π(0.01)2=π×0.0001m2≈3.14×10−4m2
Stress is defined as the force per unit area:
σ=FA
Given F=100kN=100×103N:
σ=100×1033.14×10−4≈318,471,337.58N/m2≈3.18×108N/m2
Using Young's modulus E:
E=σϵ⟹ϵ=σE
Given E=2.0×104N/m2:
ϵ=3.18×1082.0×104≈15900
The elastic energy density is given by:
EED=12σϵ
Substituting the values of σ and ϵ:
EED=12×(3.18×108)×(15900)≈2.53×1012J/m3
The elastic energy density of the steel rod is approximately:
EED≈2.5×105J/m3
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - A)
Explore 31 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - B)
Explore 15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment(Section-D)
Explore 14 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - J
Explore 9 Videos
- Mock test 03Book:AAKASH INSTITUTE ENGLISHChapter:Mock test 03Exercise:EXAMPLE
Explore 44 Videos
Similar Questions
A structural steel rod has a radius r =10mm and a length l.=1m When a force F=100kN is applied, it stretches it along its length. Young's modulus of elasticity of the structural steel is 2.0×1011Nm−2. What is the elastic energy density of the steel rod ?
View SolutionA structural steel rod has a radius r(=10 mm) and a length l(=1 m). When a force F(= 100 kN) is applied, it stretches it along its length. Young's modulus of elasticity of the structural steel is 2.0×1011Nm−2.
What is the stress produced ?
View SolutionA structural steel rod has a radius r(=10 mm) and a length l(=1 m). When a force F(= 100 kN) is applied, it stretches it along its length. Young's modulus of elasticity of the structural steel is 2.0×1011Nm−2.
What is the elongation produced ?
View SolutionA steel rod has a radius 10 mm and a length of 1.0 m. A force stretches it along its length and produces a strain of 0.32%. Young's modulus of the steel is 2.0×1011Nm−2. What is the magnitude of the force stretching the rod?
View SolutionA structural steel rod has a radius of 10 mm and a length of 1.0 m. A 100 kN force stretches it along its length. Calculate (a) stress, (b) elongation, and ( c ) strain on the rod. Young's modulus, of structural steel is 2.0 × 1011 N m−2.
View SolutionA steel rod has a radius of cross-sectional area is R= 10 mm and length L = 90 cm ls fixed at one end, a force F=3.14⋅104N stretches it along its length, the stress in the rod is equal to (take π = 3.14)
View SolutionA rod has a radius of 100 mm and a length of 10 cm. A 100 N force compresses along its length . Calculate the longitudinal stress developed in the rod.
View SolutionA rod has a radius of 100 mm and a length of 10 cm. A 100 N force compresses along its length . Calculate the longitudinal stress developed in the rod.
View SolutionConsider a rod of steel having radius of 8 mm and the length of 2 m. If a force of 150 kN stretches it along its lengths , then calculated the stress, percentage strain in the rod if the elongation in length is 7.46 mm.
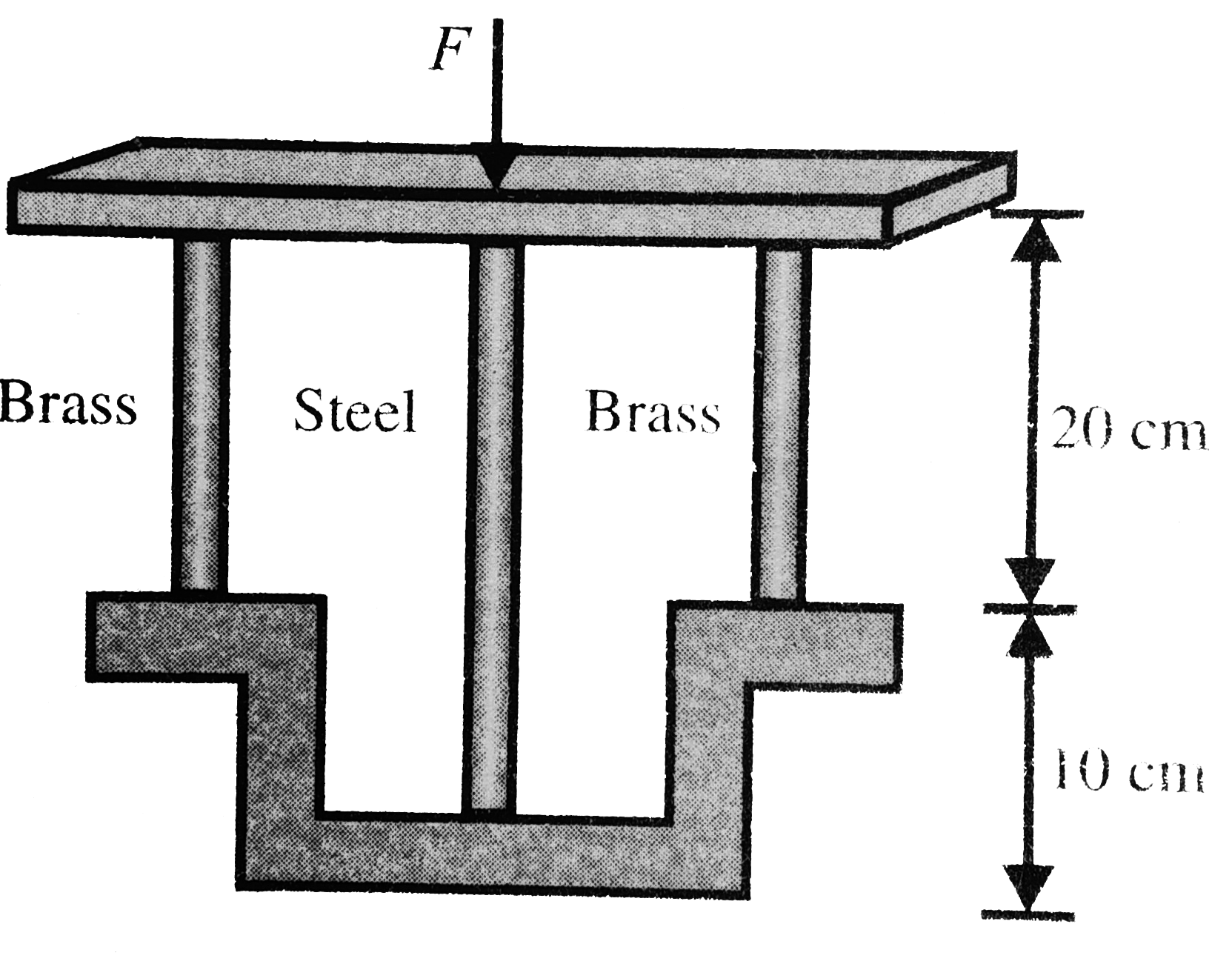
View SolutionA steel rod of length l1=30cm and two identical brass rod of length l2=20cm each support a light horizontal platform as shown in Fig. Cross-sectional area of each of the three rods is A=1cm2. A vertically downward force F=5000N is applied on the platform. Young's modulus of elasticity for steel Ys=2×1011Nm−2 and brass Yb=1×1011Nm−2. Find stress (in MPa) developed in a. Steel rod b. Brass rod
View Solution