In a series resonant LCR circuit the voltage across R is 100 volts and R = 1k(Ω)withC=2(μ)F. The resonant frequency (ω) is 200rad/s. At resonance the voltage across L is
4×10−3V
2.5×10−2V
40V
250V
The correct Answer is:D
To solve the problem, we need to find the voltage across the inductor (L) in a series resonant LCR circuit. We are given the following information:
- Voltage across the resistor (R) = 100 V
- Resistance (R) = 1 kΩ = 1000 Ω
- Capacitance (C) = 2 μF = 2 × 10^(-6) F
- Resonant frequency (ω) = 200 rad/s
1. Calculate the Current (I) in the Circuit:
The current in the circuit can be calculated using Ohm's law:
I=VRR
Where VR is the voltage across the resistor.
I=100V1000Ω=0.1A
2. Calculate the Capacitive Reactance (Xc):
The capacitive reactance Xc can be calculated using the formula:
Xc=1ωC
Substituting the given values:
Xc=1200rad/s×2×10−6F=14×10−4=2500Ω
3. Calculate the Voltage across the Capacitor (Vc):
The voltage across the capacitor can be calculated using:
Vc=I×Xc
Substituting the values we have:
Vc=0.1A×2500Ω=250V
4. Voltage across the Inductor (V_L):
At resonance, the voltage across the inductor VL is equal to the voltage across the capacitor Vc:
VL=Vc=250V
Final Answer:
The voltage across the inductor VL is 250 V.
- Resistance (R) = 1 kΩ = 1000 Ω
- Capacitance (C) = 2 μF = 2 × 10^(-6) F
- Resonant frequency (ω) = 200 rad/s
The current in the circuit can be calculated using Ohm's law:
I=VRR
Where VR is the voltage across the resistor.
I=100V1000Ω=0.1A
The capacitive reactance Xc can be calculated using the formula:
Xc=1ωC
Substituting the given values:
Xc=1200rad/s×2×10−6F=14×10−4=2500Ω
The voltage across the capacitor can be calculated using:
Vc=I×Xc
Substituting the values we have:
Vc=0.1A×2500Ω=250V
At resonance, the voltage across the inductor VL is equal to the voltage across the capacitor Vc:
VL=Vc=250V
The voltage across the inductor VL is 250 V.
Similar Questions
Knowledge Check
A series LCR circuit containing a resistance of 120Ω has angular resonance frequency 4×105rads−1. At resonance the vlotage across resistance and inductance are 60V and 40 V, repectively,
At what frequency, the current in the circuit lags the voltage bu 45∘ ?A16×105rad s−1B8×105rad s−1C4×105rad s−1D2×105rad s−1
In an L-C-R series, AC circuit at resonance
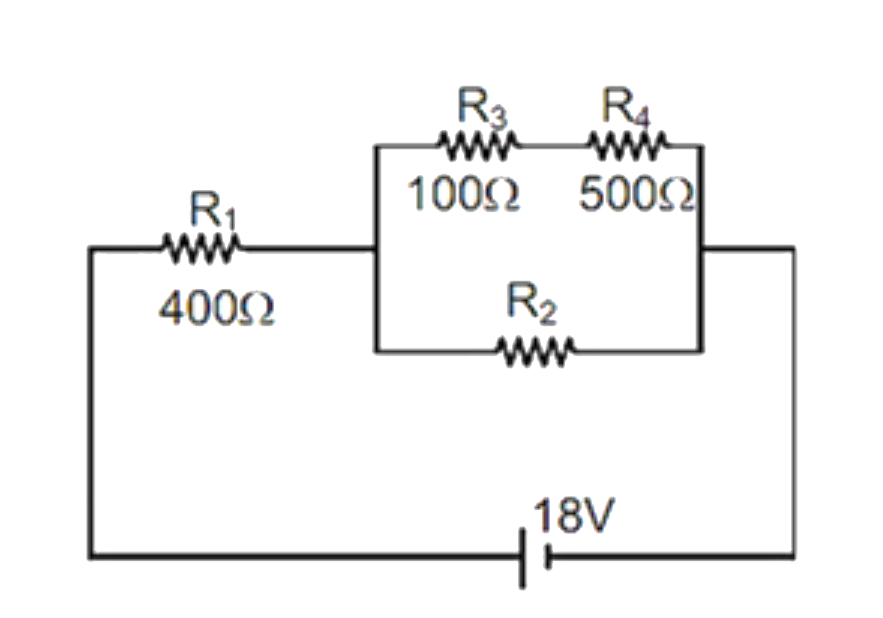
View SolutionIf the voltage across 500Ω is 5 V. then R2 is
View SolutionIn series LCR circuit, the voltages across R, L and C are shown in the figure. The voltage of applied source

View SolutionAt resonance in series R-L-C circuit
_PHY_E06_308_Q01.png)
View SolutionA series LCR circuit containing a resistance of 120Ω has angular resonance frequency 4×105rads−1. At resonance the vlotage across resistance and inductance are 60V and 40 V, repectively,
the value of inductance L is
View SolutionA series LCR circuit containing a resistance of 120Ω has angular resonance frequency 4×105rads−1. At resonance the vlotage across resistance and inductance are 60V and 40 V, repectively,
The value of capacitance C is
View SolutionIn series LCR circuit, the phase difference between voltage across L and voltage across C is
View Solution