A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

$\sqrt{3} \frac{F}{M R}$

$\frac{F}{M R}$

$\frac{2}{\sqrt{3}} \frac{F}{M R}$

$\frac{F}{2 M R}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video & image solution for A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Two equal and opposite forces F are allplied tangentially to a uniform disc of mass M and radius R . If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :
View Solution
If a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?
View Solution
A uniform disc of mass $m$ & radius $R$ is pivoted at its centre $O$ with its plane vertical as shown in figure $A$ circular portion of disc of radius $\frac{R}{2}$ is removed from it. Then choose the correct option(s)

View Solution
A uniform disc of mass $M$ and radius R is pivoted about the horizontal axis through its centre $C$ A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when $m$ reaches the bottom point B.
View Solution
A uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View Solution
Two identical uniform discs of mass $m$ and radius $r$ are arranged as shown in the figure. If $α$ is the angular acceleration of the lower disc and $a_{c m}$ is acceleration of centre of mass of the lower disc, then relation among $a_{c m}, α$ and $r$ is

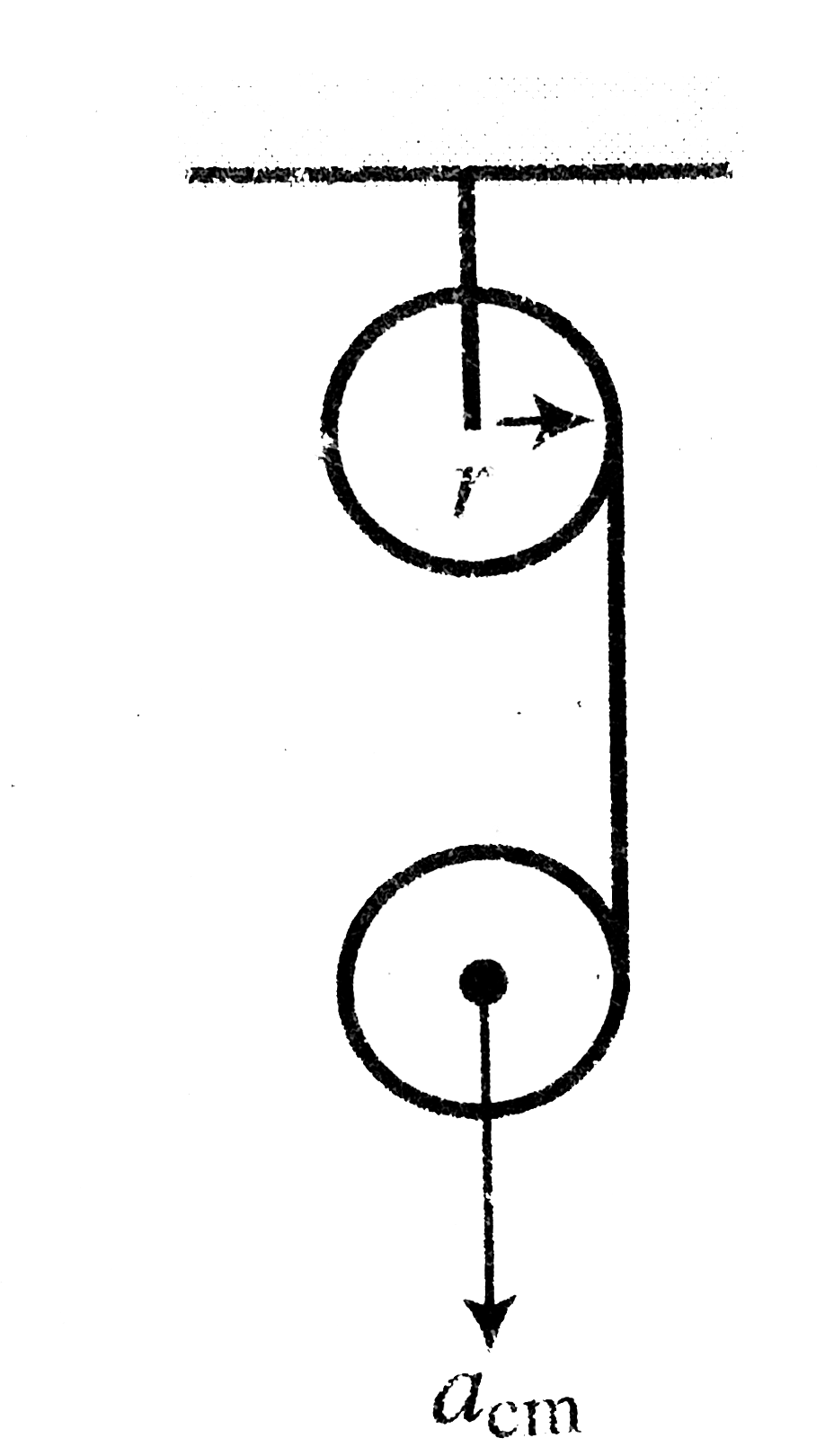
View Solution
Given a uniform disc of mass $M$ and radius $R$ . A small disc of radius $R / 2$ is cut from this disc in such a way that the distance between the centres of the two discs is $R / 2$ . Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View Solution
A uniform disc of mass $m$ and radius $R$ is pivoted smoothly at its centre of mass. A light spring of stiffness $k$ is attached with the dics tangentially as shown in the Fig. Find the angular frequency in $\frac{r a d}{s}$ of torsional oscillation of the disc. (Take $m = 5 k g$ and $K = 10 \frac{N}{m}$ .)
View Solution
A uniform disc of mass $m$ and radius $R$ is pivoted smoothly at its centre of mass. A light spring of stiffness $k$ is attached with the dics tangentially as shown in the Fig. Find the angular frequency in $\frac{r a d}{s}$ of torsional oscillation of the disc. (Take $m = 5 k g$ and $K = 10 \frac{N}{m}$ .)
View Solution
A uniform disc of mass m and radius R is pivoted at point P and is free rotate in vertical plane. The centre C of disc is initially in horizontal position with P as shown in figure. If it is released from this position, then its angular acceleration when the line PC is inclined to the horizontal at an angle $θ$ is

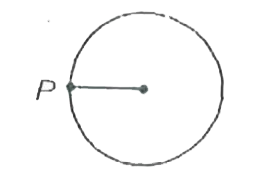
View Solution

A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

The correct Answer is:B

Similar Questions

Recommended Questions