A force F acts tangentially on a part of a uniform disc of mass 'm' an

A force $F$ acts tangentially at the highest point of a disc of mass $m$ kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:

A $\frac{2 F}{3 m}$
B $\frac{10 F}{7 m}$
Czero
D $\frac{4 F}{3 m}$
If a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?
Agr
Bg/r
C $\frac{2 g}{r}$
D2gr
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass $m$ and radius $R$ is hinged at point $A$ at its bottom and is free to rotate in the vertical plane. A force of magnitude $F$ is acting on the ring at top most point.

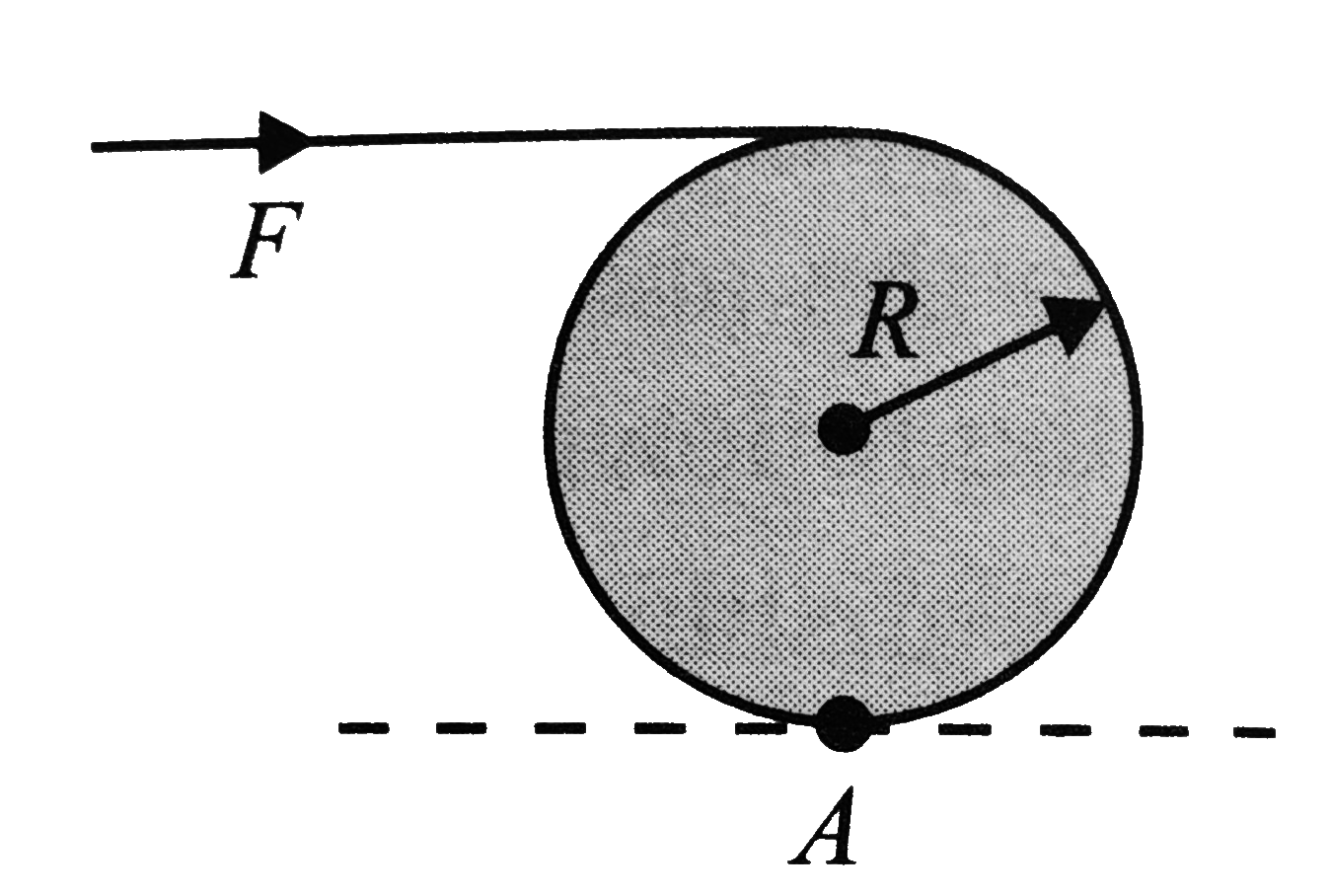
Tangential acceleration of the centre of mass is
A $\frac{3 F}{4 m}$
B $\frac{F}{m}$
C $\frac{2 F}{3 m}$
D $\frac{4 F}{3 m}$

A force F acts tangentially on a part of a uniform disc of mass 'm' and radius 'R' hinged at point O. The force exerted by hinge on the portion of disc initially.