two heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
(a)1:4
(b)1:3
(c)2:1
(d)4:1
The correct Answer is:C
To solve the problem of finding the power consumed by two resistors connected in parallel, we can follow these steps:
Step 1: Understand the Circuit Configuration
We have two resistors, R1 = 10Ω and R2 = 20Ω, connected in parallel to a battery with an EMF of 12V and an internal resistance of 1Ω.
Step 2: Calculate the Total Resistance in the Circuit
The total resistance (R_total) of the circuit can be calculated using the formula for resistors in parallel:
1Rtotal=1R1+1R2
Substituting the values:
1Rtotal=110+120
Finding a common denominator (20):
1Rtotal=220+120=320
Thus,
Rtotal=203Ω
Step 3: Calculate the Total Circuit Resistance Including Internal Resistance
Now we need to consider the internal resistance of the battery (1Ω):
Rcircuit=Rtotal+Rinternal=203+1=203+33=233Ω
Step 4: Calculate the Total Current in the Circuit
Using Ohm's Law (V = IR), we can find the total current (I) flowing through the circuit:
I=VRcircuit=12233=12×323=3623A
Step 5: Calculate the Voltage Across the Resistors
The voltage across the resistors (V_R) can be calculated using the voltage drop across the internal resistance:
Vinternal=I×Rinternal=3623×1=3623V
Thus, the voltage across the resistors is:
VR=V−Vinternal=12−3623=276−3623=24023V
Step 6: Calculate Power Across Each Resistor
Using the formula for power (P = V^2/R), we can find the power consumed by each resistor.
For R1 (10Ω):
P1=V2RR1=(24023)210=576005290W
For R2 (20Ω):
P2=V2RR2=(24023)220=5760010580W
Step 7: Find the Ratio of Power Consumed
To find the ratio of the power consumed by the two resistors:
P1P2=R2R1=2010=2:1
Conclusion
The power consumed by the two resistors is in the ratio of 2:1.
We have two resistors, R1 = 10Ω and R2 = 20Ω, connected in parallel to a battery with an EMF of 12V and an internal resistance of 1Ω.
The total resistance (R_total) of the circuit can be calculated using the formula for resistors in parallel:
1Rtotal=1R1+1R2
Substituting the values:
1Rtotal=110+120
Finding a common denominator (20):
1Rtotal=220+120=320
Thus,
Rtotal=203Ω
Now we need to consider the internal resistance of the battery (1Ω):
Rcircuit=Rtotal+Rinternal=203+1=203+33=233Ω
Using Ohm's Law (V = IR), we can find the total current (I) flowing through the circuit:
I=VRcircuit=12233=12×323=3623A
The voltage across the resistors (V_R) can be calculated using the voltage drop across the internal resistance:
Vinternal=I×Rinternal=3623×1=3623V
Thus, the voltage across the resistors is:
VR=V−Vinternal=12−3623=276−3623=24023V
Using the formula for power (P = V^2/R), we can find the power consumed by each resistor.
P1=V2RR1=(24023)210=576005290W
P2=V2RR2=(24023)220=5760010580W
To find the ratio of the power consumed by the two resistors:
P1P2=R2R1=2010=2:1
The power consumed by the two resistors is in the ratio of 2:1.
Similar Questions
Two resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionA coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The time constant of the circuit
View Solution
Knowledge Check
Three resistors of resistances 3Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 12V and negligible internal resistance, current through each resistor in ampere is
A4,3,2.4B8,7,3,4C2,5,1,8D5,5,8,2Three resistors 2Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 20V and negligible internal Resistance. The total current drawn from the battery is
A10AB15AC19AD23A
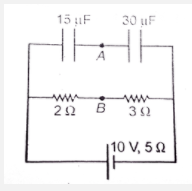
The figure shows two capacitors connected in parallel with two resistance and a battery of emf 10V , internal resistance 5Ω. At steady state.
View SolutionA coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The current in the circuit in steady state.
View SolutionA certain length of a uniform wire of resistance 12Ω is bent into a circle and two points, a quarter of circumference apart, are connected to a battery of emf 4 V and internal resistance 1Ω. Find the current in the different parts of the circuit.
View SolutionTwo resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power supplied by the battery,
View SolutionFig. shows two resistors A of 4Ω and B of 6 Ω joined in series to a battery of e.m.f. 12 V and internal resistance 2 Ω . Calculate :
the terminal voltage of the battery,
View SolutionA capacitor of capacitance 1μF is connected in parallel with a resistance 10Ω and the combination is connected across the terminals of a battery of EMF 50 V and internal resistance 1Ω. The potential difference across the capacitor at steady state is (in Volt)
View Solution
