A certain length of a uniform wire of resistance 12Ω is bent into a circle and two points, a quarter of circumference apart, are connected to a battery of emf 4 V and internal resistance 1Ω. Find the current in the different parts of the circuit.
The correct Answer is:1213A,(4)/(13)A
To solve the problem, we need to find the current in different parts of the circuit formed by a uniform wire bent into a circle, connected to a battery. Here’s a step-by-step solution:
Step 1: Understand the Circuit Configuration
The wire has a total resistance of R=12Ω and is bent into a circle. When two points on the circle are connected to a battery, which is 14 of the circumference apart, we can visualize the circuit.
Step 2: Determine the Lengths of the Wire Segments
The circumference of the circle is given by C=2πr. Since the wire is uniform, the resistance is proportional to the length. The segment connected to the battery is 14 of the circumference, and the remaining segment is 34.
- Length of segment 1 (connected to the battery): L1=L4
- Length of segment 2: L2=3L4
Step 3: Calculate the Resistances of the Segments
Using the relationship R=ρLA, we can find the resistances of the segments:
- Resistance of segment 1 (R1):
R1=12Ω4=3Ω
- Resistance of segment 2 (R2):
R2=34×12Ω=9Ω
Step 4: Analyze the Circuit with the Battery
The battery has an emf of 4V and an internal resistance of 1Ω. The total resistance in the circuit is the sum of the resistances of the segments and the internal resistance of the battery.
Step 5: Calculate the Equivalent Resistance
The equivalent resistance RAB between points A and B (where the battery is connected) is given by:
RAB=R1+R2=3Ω+9Ω=12Ω
Adding the internal resistance of the battery:
Req=RAB+Rinternal=12Ω+1Ω=13Ω
Step 6: Calculate the Total Current from the Battery
Using Ohm's law, the total current I from the battery is:
I=VReq=4V13Ω=413A
Step 7: Determine the Current Distribution
Since the resistances are in series, the current divides in the ratio of the resistances. The current I1 through R1 and I2 through R2 can be calculated using the current division rule.
Using the ratio of the resistances:
I1I2=R2R1=93=3
Let I1=3x and I2=x. Then:
I1+I2=I⟹3x+x=413⟹4x=413⟹x=113
Thus:
I1=3x=313A,I2=x=113A
Final Answer
- Current through segment 1 (I1): 313A
- Current through segment 2 (I2): 113A
The wire has a total resistance of R=12Ω and is bent into a circle. When two points on the circle are connected to a battery, which is 14 of the circumference apart, we can visualize the circuit.
The circumference of the circle is given by C=2πr. Since the wire is uniform, the resistance is proportional to the length. The segment connected to the battery is 14 of the circumference, and the remaining segment is 34.
- Length of segment 2: L2=3L4
Using the relationship R=ρLA, we can find the resistances of the segments:
R1=12Ω4=3Ω
R2=34×12Ω=9Ω
The battery has an emf of 4V and an internal resistance of 1Ω. The total resistance in the circuit is the sum of the resistances of the segments and the internal resistance of the battery.
The equivalent resistance RAB between points A and B (where the battery is connected) is given by:
RAB=R1+R2=3Ω+9Ω=12Ω
Adding the internal resistance of the battery:
Req=RAB+Rinternal=12Ω+1Ω=13Ω
Using Ohm's law, the total current I from the battery is:
I=VReq=4V13Ω=413A
Since the resistances are in series, the current divides in the ratio of the resistances. The current I1 through R1 and I2 through R2 can be calculated using the current division rule.
I1I2=R2R1=93=3
Let I1=3x and I2=x. Then:
I1+I2=I⟹3x+x=413⟹4x=413⟹x=113
Thus:
I1=3x=313A,I2=x=113A
- Current through segment 1 (I1): 313A
- Current through segment 2 (I2): 113A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-6
5 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-3
4 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
A wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are

View SolutionA wire of resistance 4Ω is bent to form a circle. The resistance point A and B will be
_PHY_E05_303_Q01.png)
View Solution
Knowledge Check
A uniform wire of resistance 36Ω is bent in the form of a circle. The effective resistance across the points A and B is
 A5ΩB15ΩC7.2ΩD30Ω
A5ΩB15ΩC7.2ΩD30Ω
A coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The time constant of the circuit
View Solutiontwo heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionA coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The current in the circuit in steady state.
View SolutionA uniform wire of resistance 18Ω is bent in the form of a circle. The effective resistance across the points a and b is
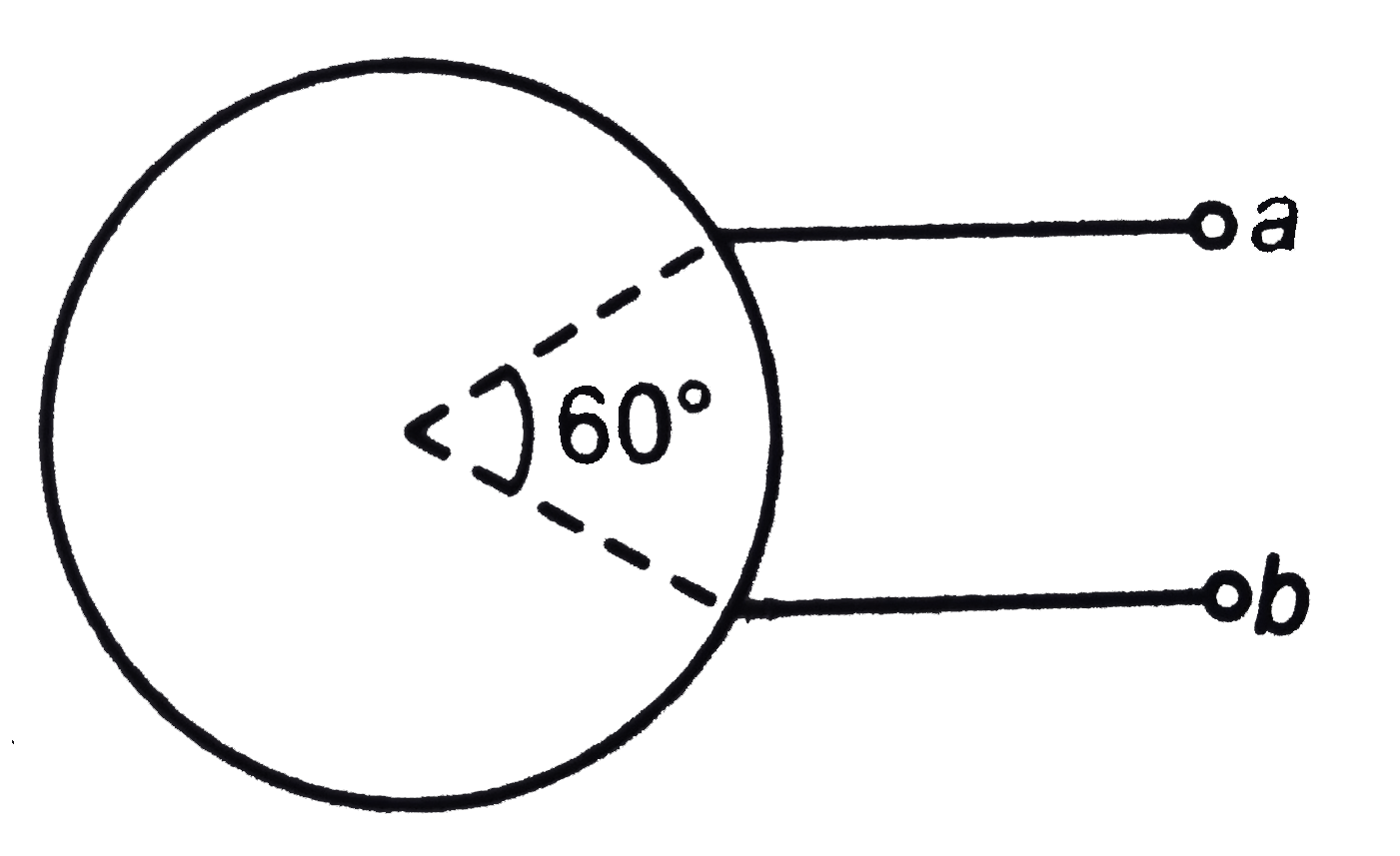
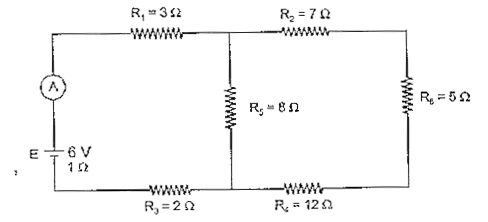
View SolutionIn the circuit shown below, E is a battery of emf 6 V and internal resistance 1Ω. Find the reading of the ammeter A. if it has negligible resistance :
View SolutionA potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View Solution
