The normal reaction on a body placed in a lift moving up with constant acceleration 2ms−1 is 120 N. Mass of the body is (Take g=10ms−2)
10 kg
15 kg
12 kg
5 kg
The correct Answer is:A
Step by step video & image solution for The normal reaction on a body placed in a lift moving up with constant acceleration 2ms^(-1) is 120 N. Mass of the body is (Take g = 10ms^(-2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
A body under the action of a force →F=6ˆi−8ˆjN acquires an acceleration of 5ms−2 . The mass of the body is
A2kgB5kgC4kgD6kg - Question 2 - Select One
A rocket with a lift-off mass 2×104kg is blasted upwards with an initial acceleration of 5ms−2. The initial thrust of the blast is (Take g=10ms−2)
A2×105NB3×105NC4×105ND5×105N - Question 3 - Select One
The person o( mass 50 kg slands on a weighing scale on a lift. If the lift is ascending upwards with a uniform acceleration of 9ms−2, what would be the reading of the weighting scale? (Take g=10ms−2)
A50kgB60kgC96kgD176kg
The apparent weight of man inside a lift moving up with certain acceleration is 900N. When the lift is coming down with the same acceleration apparent weight is found to be 300N. The mass of the man is (g = 10ms−2)
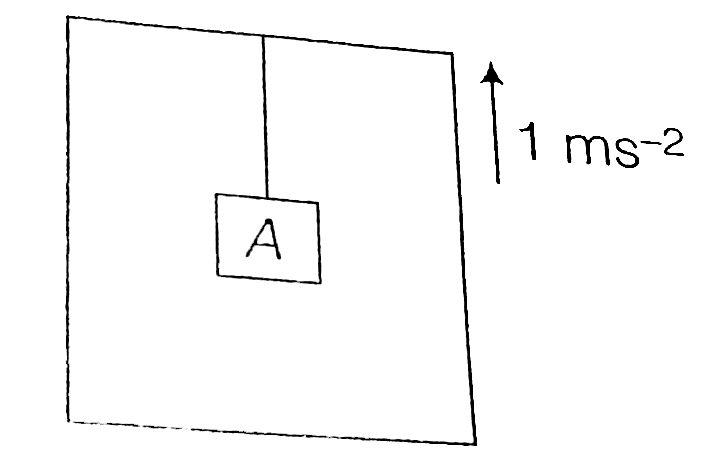
View SolutionIf the elevator in shown figure is moving upwards with constant acceleration 1ms−2, tension in the string connected to block A of mass 6 kg would be ( take, g=10ms−2)
 View Solution
View SolutionCalculate the work done in lifting a 300N weight to a height of 10m with an acceleration 0.5ms−2. Take g=10ms−2.
View SolutionA person of mass 50 kg stands on a weighing scale on a lift . If the lift is descending with a downward acceleration of 9ms−2 what would be the reading of the weighing scale? (g=10ms−2) .
View SolutionA person of mass 50 kg stands on a weighing scale on a lift . If the lift is descending with a downward acceleration of 9ms−2 what would be the reading of the weighing scale? (g=10ms−2) .
View Solution
