In a radioactive disintegration, the ratio of initial number of atoms to the number of atoms present at an instant of time equal to its mean life is
1e2
1e
e
e2
The correct Answer is:C
To solve the problem, we need to find the ratio of the initial number of atoms (N₀) to the number of atoms present at an instant of time equal to its mean life (τ). Here are the steps to derive the solution:
1. Understand the Mean Life (τ):
The mean life (τ) of a radioactive substance is defined as the average time that a particle exists before it decays. It is given by the formula:
τ=1λ
where λ is the decay constant.
2. Radioactive Decay Formula:
The number of atoms remaining (N) after time t can be expressed using the radioactive decay formula:
N=N0e−λt
where:
- N0 = initial number of atoms
- N = number of atoms remaining after time t
- e = base of the natural logarithm
- λ = decay constant
- t = time elapsed
3. Substituting Mean Life into the Formula:
Since we are interested in the case where t=τ, we substitute t with τ:
N=N0e−λτ
Now, substituting τ=1λ:
N=N0e−λ(1λ)=N0e−1
4. Finding the Ratio:
Now, we need to find the ratio of the initial number of atoms to the number of atoms remaining after time τ:
N0N=N0N0e−1=e
5. Conclusion:
Therefore, the ratio of the initial number of atoms to the number of atoms present at an instant of time equal to its mean life is:
N0N=e
Final Answer:
The answer is e.
The mean life (τ) of a radioactive substance is defined as the average time that a particle exists before it decays. It is given by the formula:
τ=1λ
where λ is the decay constant.
The number of atoms remaining (N) after time t can be expressed using the radioactive decay formula:
N=N0e−λt
where:
- N0 = initial number of atoms
- N = number of atoms remaining after time t
- e = base of the natural logarithm
- λ = decay constant
- t = time elapsed
Since we are interested in the case where t=τ, we substitute t with τ:
N=N0e−λτ
Now, substituting τ=1λ:
N=N0e−λ(1λ)=N0e−1
Now, we need to find the ratio of the initial number of atoms to the number of atoms remaining after time τ:
N0N=N0N0e−1=e
Therefore, the ratio of the initial number of atoms to the number of atoms present at an instant of time equal to its mean life is:
N0N=e
The answer is e.
Similar Questions
The total number of N - atoms present in veronal is
View SolutionHow is the mass of an element related to the number of atoms present in it ?
View SolutionThe rate of disintegration of a radioactive substance is …………………………… to the number of atoms present at that time .
View SolutionAtomic number is equal to the
View SolutionAtomic number of an ion is the same as the number of electrons present in it.
View SolutionThe number of atoms present in one molecule of an element is called its______
View Solution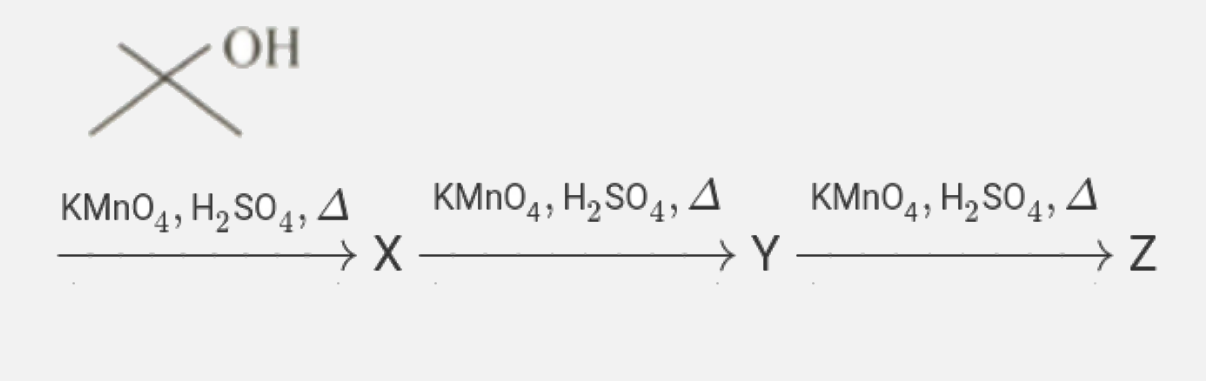
The number of C - atoms present in the final product 'Z' is
View SolutionIf the atomic number of an element is 36, the number of electrons present in the M-shell is
View SolutionNumber of iron atoms present in haemoglobin molecule is
View SolutionThe number of particles presents in 1 mol of nitrogen atom are
View Solution
