Consider the show glass slab having a thin biconvex cavity of air centred at O. A black spot at P will have image ( μglass=32 ,the radius of curvature of each surface of the cavity = 10 cm)
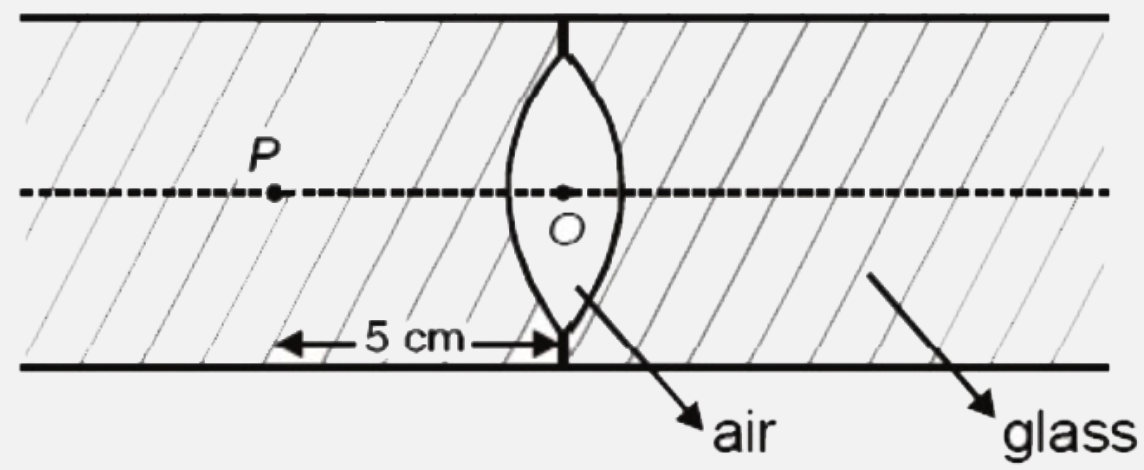
7.5 cm on the right side of O
7.5 cm on the left side of O
3.75 cm on the right side of O
3.75 cm on the left side of O
The correct Answer is:D
Step by step video & image solution for Consider the show glass slab having a thin biconvex cavity of air centred at O. A black spot at P will have image ( mu_("glass") =3/2 ,the radius of curvature of each surface of the cavity = 10 cm) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
An image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View SolutionFocal length of a thin lens in air is 10cm. Now, medium on one side of the lens is replaced by a medium of refractive inidex μ=2. The radius of curvature of the surface of lens, in contact with the medium, is 20cm. Find the new focal length.
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.

View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.

View SolutionShow that for refraction at a concave spherical surface (separating glass-air medium), the distance of the object should be greater than three times the radius of curvature of the refracting surface for the image to be real.
View SolutionA beam of light coming from infinty is passing through a biconvex lens having radius of curvature R=20cm of each surface, if focused at a certain distance from lens. Find the radius of curvature of emergent wave front from lens : (μ≤ns=1.5)
View SolutionTwo converging glass lenses A and B have focal lengths in the ratio 2:1. The radius of curvature of first surface of lens A is 1/4 th of the second surface where as the radius of curvature of first surface of lens B is twice that of second surface. Then the ratio between the radii of the first surfaces of A and B is
View SolutionA hollow sphere of glass of R.I .n has small mark M on its interior surface which is observed by an observer O from a point outside the sphere, .C is centre of the sphere. The inner cavity (air) is concentric with the external surface and thickness of the glass is every where equal to the radius of the inner surface. Find the distance by which the mark will appear nearer than it really is in terms of n and R assuming paraxial rays.
_E01_156_Q01.png)
View SolutionA plano-convex lens P and a concavo-convex lens Q are in contact as shown in figure. The refractive index o fthe material of the lens P and Q is 1.8and1.2 respectively. The radius of curvature of the concave surface of the lens Q is double the radius of curvature of the convex surface. The convex surface of Q is silvered.

An object is placed on the placed on the principal axis at a distance 10cm form the plane surface. The image is formed at a distance 40cm from the plane surfaces on the same side. The focal length of the system is
View Solution
