In Young's double slit experiment the light emitted from source has λ=6500Å and the distance between th two slits is 1 mm. Distance between the screen and slit is 1 metre. Distance between third dark and fifth birth fringe will be :
3.2 mm
1.63 mm
0.585 mm
2.31 mm
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Convert the given wavelength into meters
The wavelength of the light is given as λ=6500Å.
1 Ångström (Å) = 10−10 meters, so:
λ=6500Å=6500×10−10m=6.5×10−7m
Step 2: Identify the distances
The distance between the two slits is given as d=1mm:
d=1mm=1×10−3m
The distance between the screen and the slits is given as D=1m.
Step 3: Calculate the position of the fifth bright fringe
The position of the n-th bright fringe is given by the formula:
yn=nλDd
For the fifth bright fringe (n=5):
y5=5×(6.5×10−7)×11×10−3=5×6.5×10−4=3.25×10−3m=3250mm
Step 4: Calculate the position of the third dark fringe
The position of the n-th dark fringe is given by the formula:
ydark=(2n−1)λD2d
For the third dark fringe (n=3):
y3=(2×3−1)×(6.5×10−7)×12×(1×10−3)=5×(6.5×10−7)×12×10−3=32.5×10−72×10−3=16.25×10−4m=1.625mm
Step 5: Calculate the distance between the third dark fringe and the fifth bright fringe
Now, we find the distance between the fifth bright fringe and the third dark fringe:
Distance=y5−y3=3.25mm−1.625mm=1.625mm
Final Answer
The distance between the third dark fringe and the fifth bright fringe is 1.625mm.
---
The wavelength of the light is given as λ=6500Å.
λ=6500Å=6500×10−10m=6.5×10−7m
The distance between the two slits is given as d=1mm:
d=1mm=1×10−3m
The position of the n-th bright fringe is given by the formula:
yn=nλDd
For the fifth bright fringe (n=5):
y5=5×(6.5×10−7)×11×10−3=5×6.5×10−4=3.25×10−3m=3250mm
The position of the n-th dark fringe is given by the formula:
ydark=(2n−1)λD2d
For the third dark fringe (n=3):
y3=(2×3−1)×(6.5×10−7)×12×(1×10−3)=5×(6.5×10−7)×12×10−3=32.5×10−72×10−3=16.25×10−4m=1.625mm
Now, we find the distance between the fifth bright fringe and the third dark fringe:
Distance=y5−y3=3.25mm−1.625mm=1.625mm
The distance between the third dark fringe and the fifth bright fringe is 1.625mm.
Similar Questions
In Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double slit experiment, the distance between two slits is made three times then the fringe width will becomes
View SolutionIn Young's double slit experiement when wavelength used is 6000Å and the screen is 40cm from the slits, the fringes are 0.012cm wide. What is the distance between the slits?
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
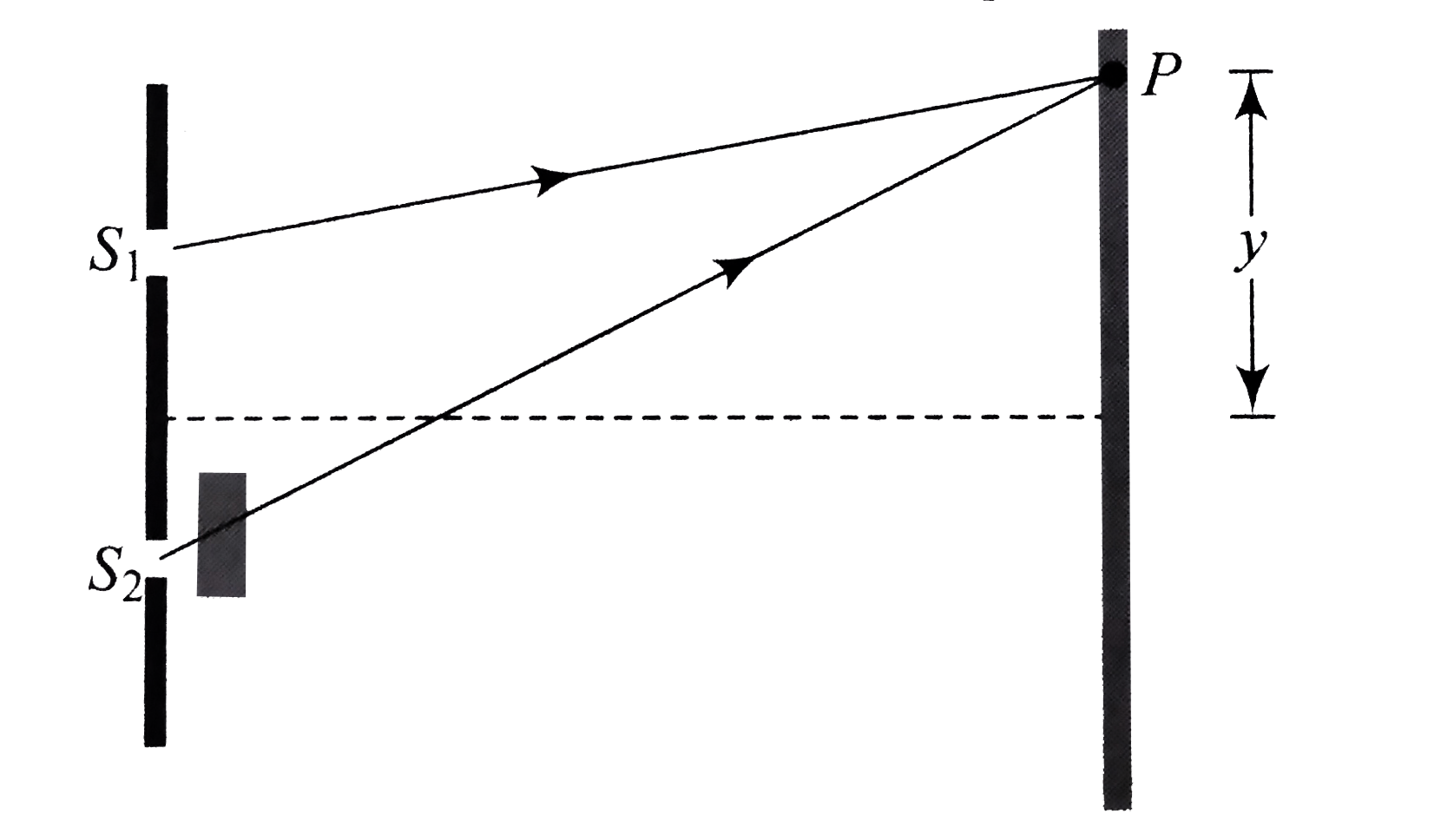
The value of η is
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
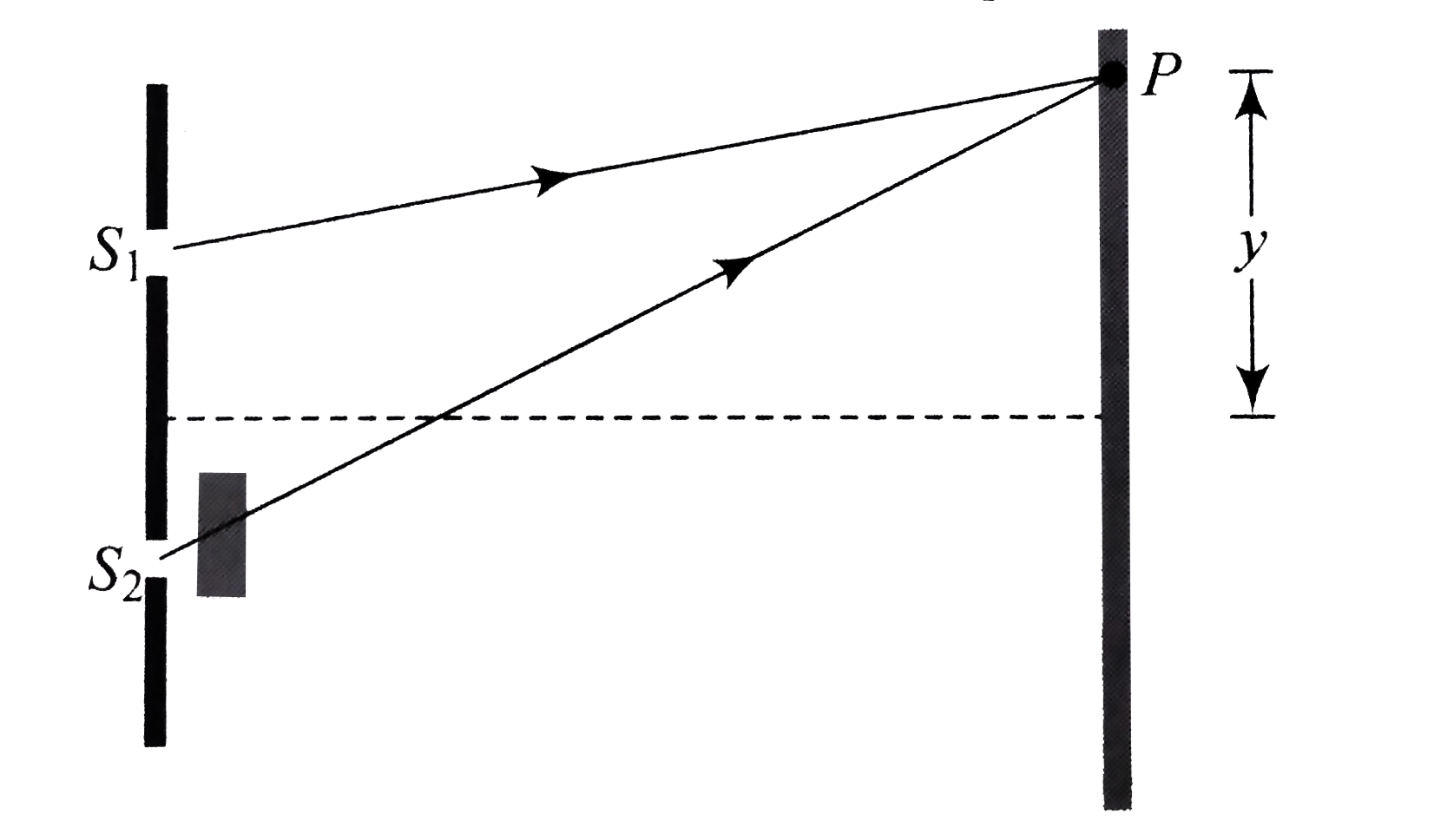
Intensity at point P is
View SolutionA beam of light consisting of two wavelenths, 6500 Å and 5200 Å is used to obtain interference fringes in a Young's double slit experiment (1Å=10−10m). The distance between the slits is 2.0 mm and the distance between the plane of the slits and the screen in 120 cm. (a) Find the distance of the third bright frings on the screen from the central maximum for the wavelength 6500 Å (b) What is the least distance from the central maximum where the bright frings due to both the wavlelengths coincide ?
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View Solution
