Two particles of masses ma and mb and same charge are projected in a perpendicular magnetic field . They travel along circular paths of radius ra and rb such that ra>rb . Then which is true ?
mava>mbvb
ma>mbandva>vb
ma=mbandva=vb
mbvb>mava
The correct Answer is:A
To solve the problem, let's analyze the motion of two charged particles in a magnetic field and derive the relationship between their masses and velocities based on the given conditions.
1. Understanding the Forces:
When a charged particle moves in a magnetic field, it experiences a magnetic force that acts as the centripetal force required for circular motion. The magnetic force FB is given by:
FB=qvB
where q is the charge of the particle, v is its velocity, and B is the magnetic field strength.
2. Centripetal Force:
The centripetal force FC required to keep a particle moving in a circular path of radius R is given by:
FC=mv2R
where m is the mass of the particle and v is its velocity.
3. Equating Forces:
For a particle to move in a circular path in a magnetic field, the magnetic force must equal the centripetal force:
qvB=mv2R
4. Rearranging the Equation:
We can rearrange this equation to express the radius R in terms of mass m and velocity v:
R=mvqB
5. Applying to Both Particles:
For particle A with mass ma and radius ra:
ra=mavaqB
For particle B with mass mb and radius rb:
rb=mbvbqB
6. Given Condition:
We know that ra>rb. Therefore:
mavaqB>mbvbqB
Since q and B are the same for both particles, we can cancel them out:
mava>mbvb
7. Conclusion:
This implies that the product of mass and velocity for particle A is greater than that for particle B. Thus, the correct relationship is:
mava>mbvb
Final Answer:
The correct option is that mava>mbvb.
When a charged particle moves in a magnetic field, it experiences a magnetic force that acts as the centripetal force required for circular motion. The magnetic force FB is given by:
FB=qvB
where q is the charge of the particle, v is its velocity, and B is the magnetic field strength.
The centripetal force FC required to keep a particle moving in a circular path of radius R is given by:
FC=mv2R
where m is the mass of the particle and v is its velocity.
For a particle to move in a circular path in a magnetic field, the magnetic force must equal the centripetal force:
qvB=mv2R
We can rearrange this equation to express the radius R in terms of mass m and velocity v:
R=mvqB
For particle A with mass ma and radius ra:
ra=mavaqB
For particle B with mass mb and radius rb:
rb=mbvbqB
We know that ra>rb. Therefore:
mavaqB>mbvbqB
Since q and B are the same for both particles, we can cancel them out:
mava>mbvb
This implies that the product of mass and velocity for particle A is greater than that for particle B. Thus, the correct relationship is:
mava>mbvb
The correct option is that mava>mbvb.
Similar Questions
Knowledge Check
When a charged particle is projected perpendicular to a uniform magnetic field, it describes a circular path in which :
Aits speed remains constant.Bits velocity remains constant.Cits momentum remains constant.Dits kinetic energy increases.
Two prticles A and B having equal charges, after being accelerated through the same potential difference enter into a ragion of uniform magnetic field and the particles describe circular paths of radii R1andR2 respectively. The ratio of the masses of A and B is
View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then

View SolutionThe charge on a particle Y is double the charge on particle X.These two particles X and Y after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionTwo particles of equal masses are revolving in circular paths of radii r1 and r2 respectively with the same speed. The ratio of their centripetal force is
View SolutionTwo particles A and B of masses mAandmB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vAandvB respectively and the trajectories are as shown in the figure. Then -
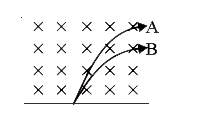
View SolutionA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View Solution
