A charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
Bq2πm
Bq2πm
2πmBq
Bq2πq
The correct Answer is:A
To find the frequency of revolution of a charged particle moving in a uniform magnetic field, we can follow these steps:
Step 1: Understand the relationship between frequency, angular velocity, and time period.
The frequency f of revolution is defined as the reciprocal of the time period T:
f=1T
The time period T can also be expressed in terms of angular velocity ω:
T=2πω
Thus, we can express the frequency in terms of angular velocity:
f=ω2π
Step 2: Determine the expression for angular velocity ω.
In circular motion, the centripetal force required to keep the particle moving in a circle is provided by the magnetic force acting on the charged particle. The magnetic force FB acting on the particle is given by:
FB=qvB
where v is the velocity of the particle and B is the magnetic field strength.
This magnetic force acts as the centripetal force, which can be expressed as:
Fc=mv2r
where m is the mass of the particle and r is the radius of the circular path.
Step 3: Set the magnetic force equal to the centripetal force.
Equating the two forces gives:
qvB=mv2r
Step 4: Solve for the velocity v.
Rearranging the equation to solve for v:
qvB=mv2r⟹qB=mvr⟹v=qBrm
Step 5: Substitute v into the expression for angular velocity ω.
The angular velocity ω is related to the linear velocity v and the radius r by the relation:
ω=vr
Substituting the expression for v:
ω=qBrm⋅1r=qBm
Step 6: Substitute ω into the frequency formula.
Now substituting ω into the frequency formula:
f=ω2π=qBm⋅2π
Final Result:
Thus, the frequency of revolution of the charged particle in the magnetic field is:
f=qB2πm
The frequency f of revolution is defined as the reciprocal of the time period T:
f=1T
The time period T can also be expressed in terms of angular velocity ω:
T=2πω
Thus, we can express the frequency in terms of angular velocity:
f=ω2π
In circular motion, the centripetal force required to keep the particle moving in a circle is provided by the magnetic force acting on the charged particle. The magnetic force FB acting on the particle is given by:
FB=qvB
where v is the velocity of the particle and B is the magnetic field strength.
Fc=mv2r
where m is the mass of the particle and r is the radius of the circular path.
Equating the two forces gives:
qvB=mv2r
Rearranging the equation to solve for v:
qvB=mv2r⟹qB=mvr⟹v=qBrm
The angular velocity ω is related to the linear velocity v and the radius r by the relation:
ω=vr
Substituting the expression for v:
ω=qBrm⋅1r=qBm
Now substituting ω into the frequency formula:
f=ω2π=qBm⋅2π
Thus, the frequency of revolution of the charged particle in the magnetic field is:
f=qB2πm
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Taking it together
Explore 75 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Assertion and reason
Explore 20 Videos
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:INTERFERENCE AND DIFFRACTION OF LIGHTExercise:Level 2 Subjective
Explore 5 Videos
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
Similar Questions
A charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View SolutionA small particle of mass m = 1 kg and charge of 1C enters perpendicularly in a triangular region of uniform magnetic field of strength 2T as shown in figure :

In the previous question find the change in angular momentum of particle w.r.t centre of its circular path during its motion in magnetic field :
View SolutionA charged particle of mass m and charge q is projected into a uniform magnetic field of induciton →B with speed v which is perpendicular to →B. The width of the magnetic field is d. The impulse imparted to the particle by the field is (d<<mv/qB)
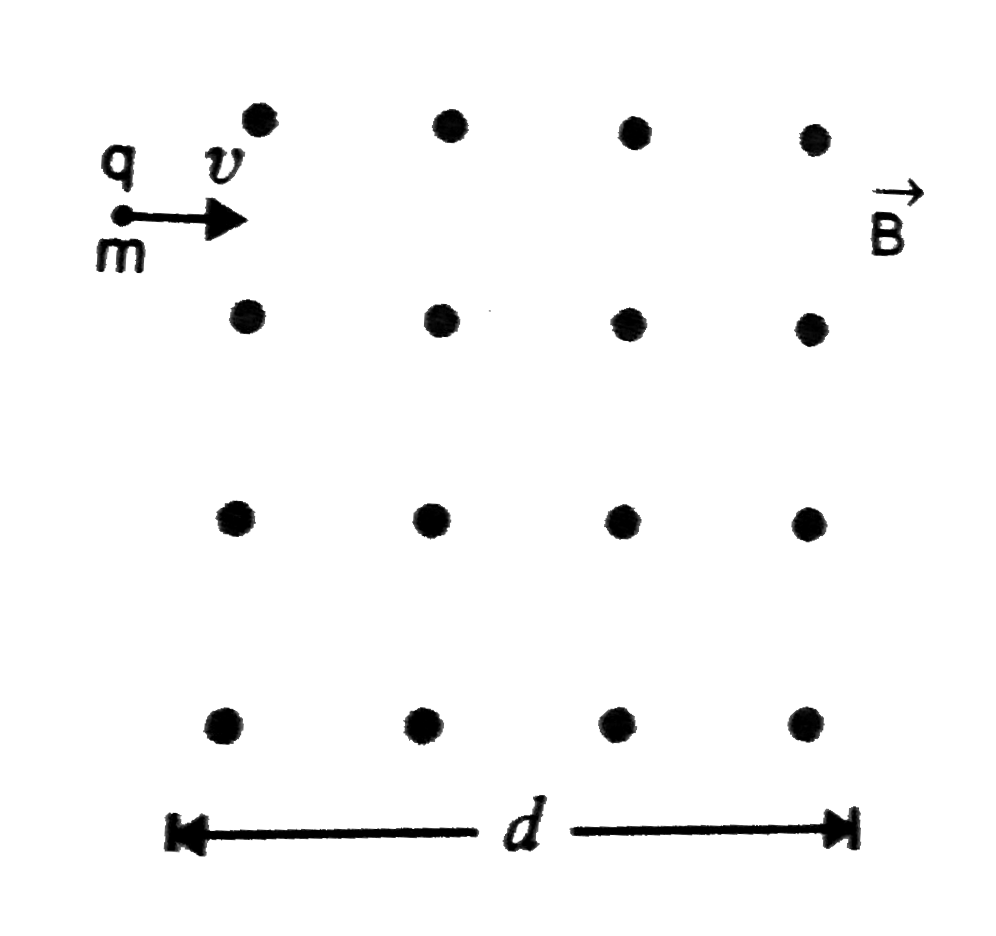
View SolutionA charge particle of mass m and charge q enters in a region of uniform magnetic field as shown in figure.The magnitude of change in linear momentum due to magnetic field will be
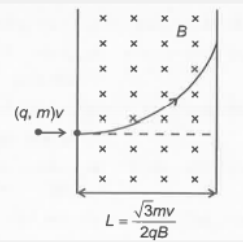
View SolutionA particle of mass m and having charge q is moving in a circular path of radius r in the presence of a uniform magnetic field. The particle breaks into smaller fragments X and Y of equal mass. The fragment X now has charge q3 and the fragment Y has charge 2q3. Immediately after the fragmentation, X comes to rest. The radius of the path of Y is now rY. The ratio rYr is ______________.
View SolutionA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle is E, then frequency of rotation is
View SolutionA charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
View SolutionThe time period of a charged particle undergoing a circular motion in a uniform magnetic field is independent of its
View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View SolutionA charged particle is moving in a circular path in uniform magnetic field. Match the following.

View Solution
