If the coefficient of friction between the wedge A and block B shown in the figure is μ, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45∘ ]
![If the coefficient of friction between the wedge A and block B shown in the figure is mu, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45^@ ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NTA_NEET_SET_78_E01_023_Q01.png)
μg
g(1+μ1−μ)
gμ
g(1−μ1+μ)
The correct Answer is:B
Step by step video & image solution for If the coefficient of friction between the wedge A and block B shown in the figure is mu, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45^@ ] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is
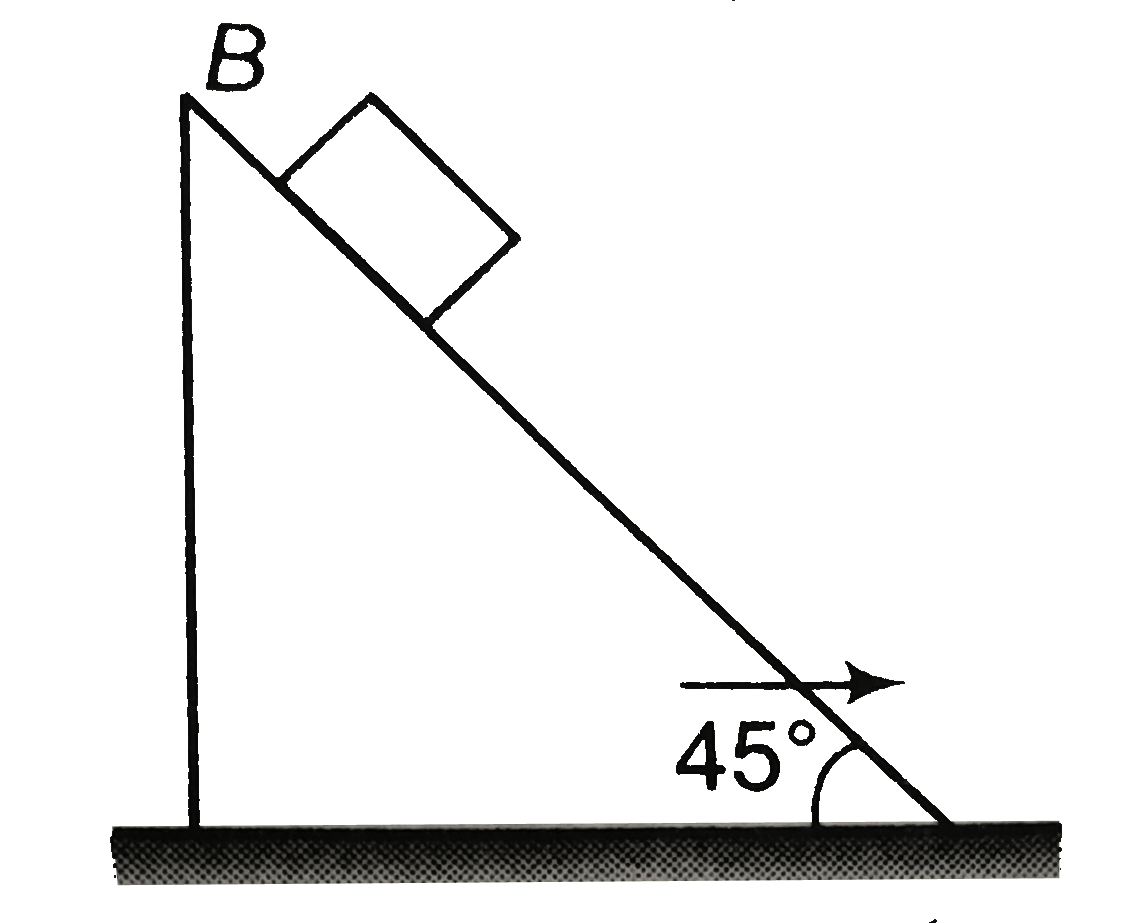
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View Solution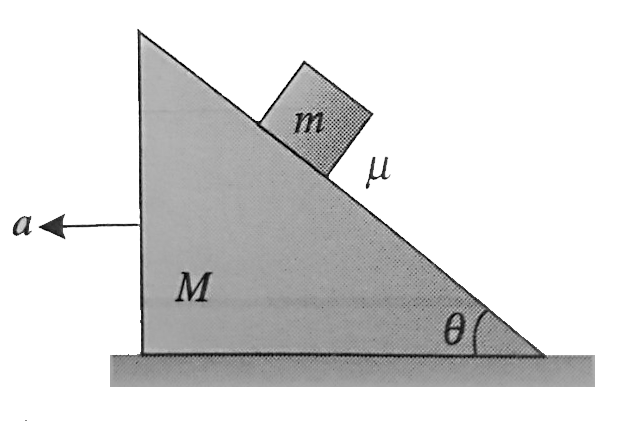
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View SolutionIn the adjoining figure, the coefficient of friction between wedge (of mass M) and block (of mass m) is μ.
Find the minimum horizontal force F required to keep the block stationary with respect to wedge.

View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionA ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.

View SolutionFour block are arranged on a smooth horizontal surface as shown in figure .The masses of the blocks are given (see the fig ) The coefficient of static friction between the top and the bottom blocks is μs What is the maximum value of the horizontal force F applied to one of the bottom blocks as shown that makes all four block with the same acceleration ?

View Solution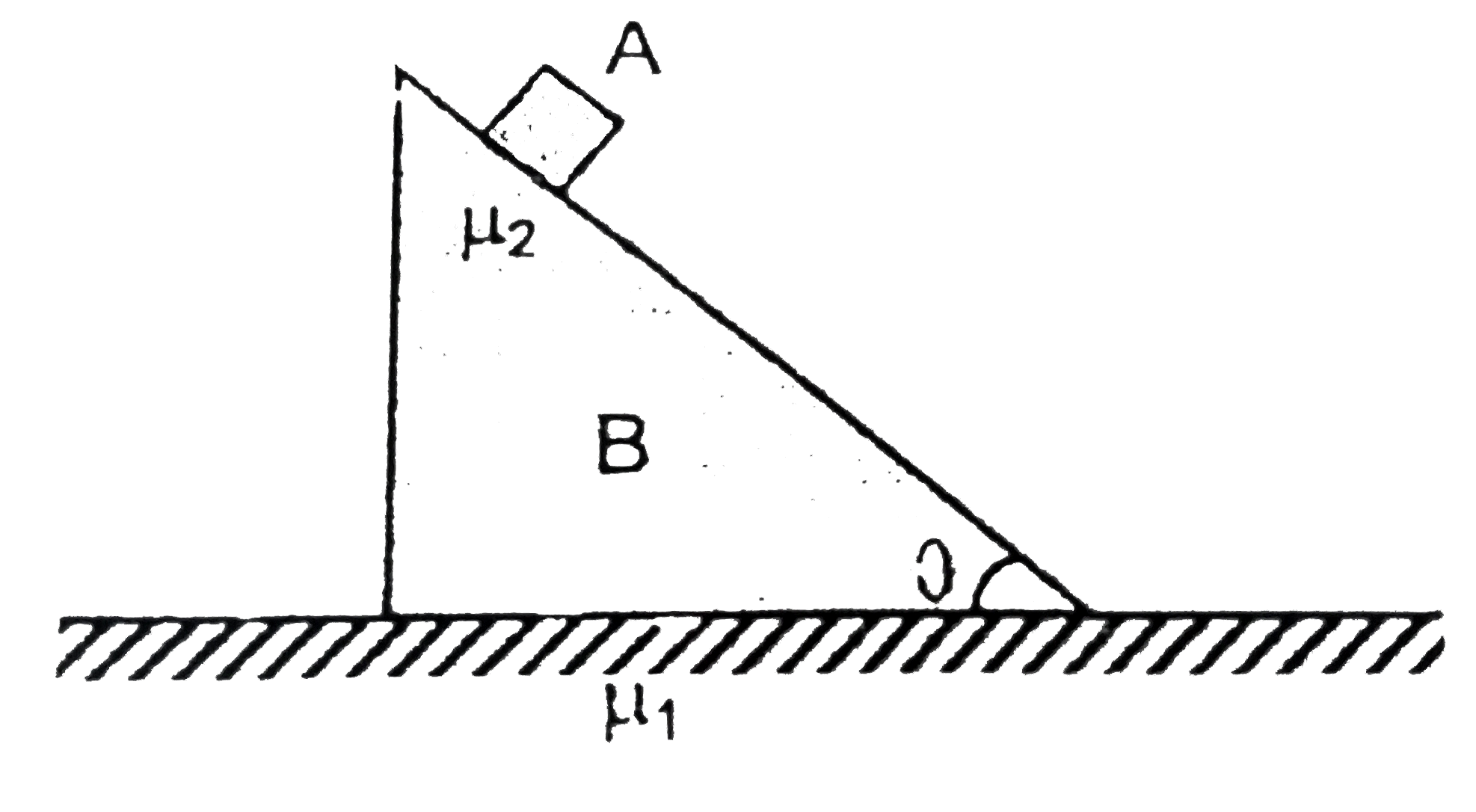
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View Solution
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
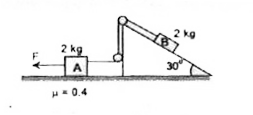
View SolutionIn the figure shown coefficient of friction between block A and ground is 0.4 and that between wedge and block B is zero. Wedge is fixed. Find tension is string and acceleration of block A if F = 28 N.
View Solution
