Two simple pendulum first of bob mass M1 and length L1 second of bob mass M2 and length L2M1=M2 and L1 = 2L_(2). if the vibrational energy of both is same which is correct?
Amplitude of B is smaller than A
Amplitude of B is greater than A
Amplitude will be same
None of the above
The correct Answer is:A
To solve the problem step by step, we will analyze the given information and apply the relevant formulas.
Step 1: Understand the given information
We have two simple pendulums:
- Pendulum 1: Bob mass M1 and length L1
- Pendulum 2: Bob mass M2 and length L2
Given:
- M1=M2
- L1=2L2
Step 2: Write the formula for frequency of a simple pendulum
The frequency f of a simple pendulum is given by the formula:
f=12π√gL
where g is the acceleration due to gravity and L is the length of the pendulum.
Step 3: Find the frequencies of both pendulums
For Pendulum 1:
f1=12π√gL1
For Pendulum 2:
f2=12π√gL2
Step 4: Establish the relationship between the frequencies
Using the relationship between the lengths:
L1=2L2
We can express the frequency ratio:
f1f2=√L2L1=√L22L2=√12=1√2
Step 5: Relate the frequencies
From the frequency ratio, we can express:
f1=1√2f2
This implies:
f2=√2f1
Step 6: Write the expression for vibrational energy
The vibrational energy E of a pendulum is given by:
E=12mA2ω2
where A is the amplitude and ω=2πf.
Step 7: Set the energies equal
Since the vibrational energies of both pendulums are the same:
E1=E2
This leads to:
12M1A21(2πf1)2=12M2A22(2πf2)2
Step 8: Substitute the known values
Since M1=M2:
A21(2πf1)2=A22(2πf2)2
This simplifies to:
A21f21=A22f22
Step 9: Express amplitudes in terms of frequencies
Rearranging gives:
A21A22=f22f21
Substituting f2=√2f1:
A21A22=(√2f1)2f21=2
Thus:
A21=2A22⟹A1=√2A2
Conclusion
Since A1>A2, we can conclude that the amplitude of Pendulum 1 is greater than that of Pendulum 2.
We have two simple pendulums:
- Pendulum 1: Bob mass M1 and length L1
- Pendulum 2: Bob mass M2 and length L2
- M1=M2
- L1=2L2
The frequency f of a simple pendulum is given by the formula:
f=12π√gL
where g is the acceleration due to gravity and L is the length of the pendulum.
For Pendulum 1:
f1=12π√gL1
f2=12π√gL2
Using the relationship between the lengths:
L1=2L2
We can express the frequency ratio:
f1f2=√L2L1=√L22L2=√12=1√2
From the frequency ratio, we can express:
f1=1√2f2
This implies:
f2=√2f1
The vibrational energy E of a pendulum is given by:
E=12mA2ω2
where A is the amplitude and ω=2πf.
Since the vibrational energies of both pendulums are the same:
E1=E2
This leads to:
12M1A21(2πf1)2=12M2A22(2πf2)2
Since M1=M2:
A21(2πf1)2=A22(2πf2)2
This simplifies to:
A21f21=A22f22
Rearranging gives:
A21A22=f22f21
Substituting f2=√2f1:
A21A22=(√2f1)2f21=2
Thus:
A21=2A22⟹A1=√2A2
Since A1>A2, we can conclude that the amplitude of Pendulum 1 is greater than that of Pendulum 2.
Similar Questions
Knowledge Check
- Question 1 - Select One
A simple pendulum of length 1 m has a wooden bob of mass 1 kg. It is struck by a bullet of mass 10−2 kg moving with a speed of 2×102ms−1. The height to which the bob rises before swinging back is (Take g=10ms−2)
A0.2 mB0.6 mC8 mD1 m
If the direction cosines of two lines are l1,m1,n1 and l2,m2,n2, then find the direction cosine of a line perpendicular to these lines.
View SolutionA pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
View SolutionA pendulum consists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1. The bullet emerges out of the bob with a speed of (v1)/3 and the bob just completes motion along a vertical circle, then v1 is
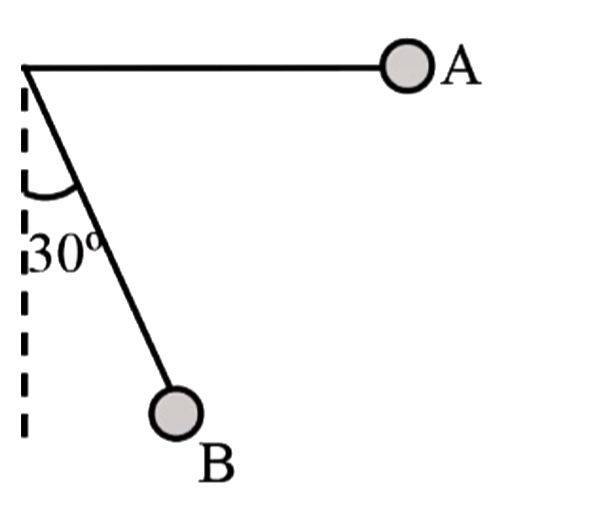
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
 View Solution
View SolutionA rod of length L is composed of a uniform length 1/2 L of wood mass is mw and a uniform length 1/2 L of brass whose mass is mb. The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
View SolutionIf <l1,m1,n1>and<l2,m2,n2> be the direction cosines of two lines L1andL2 respectively. If the angle between them is θ, the cosθ=?
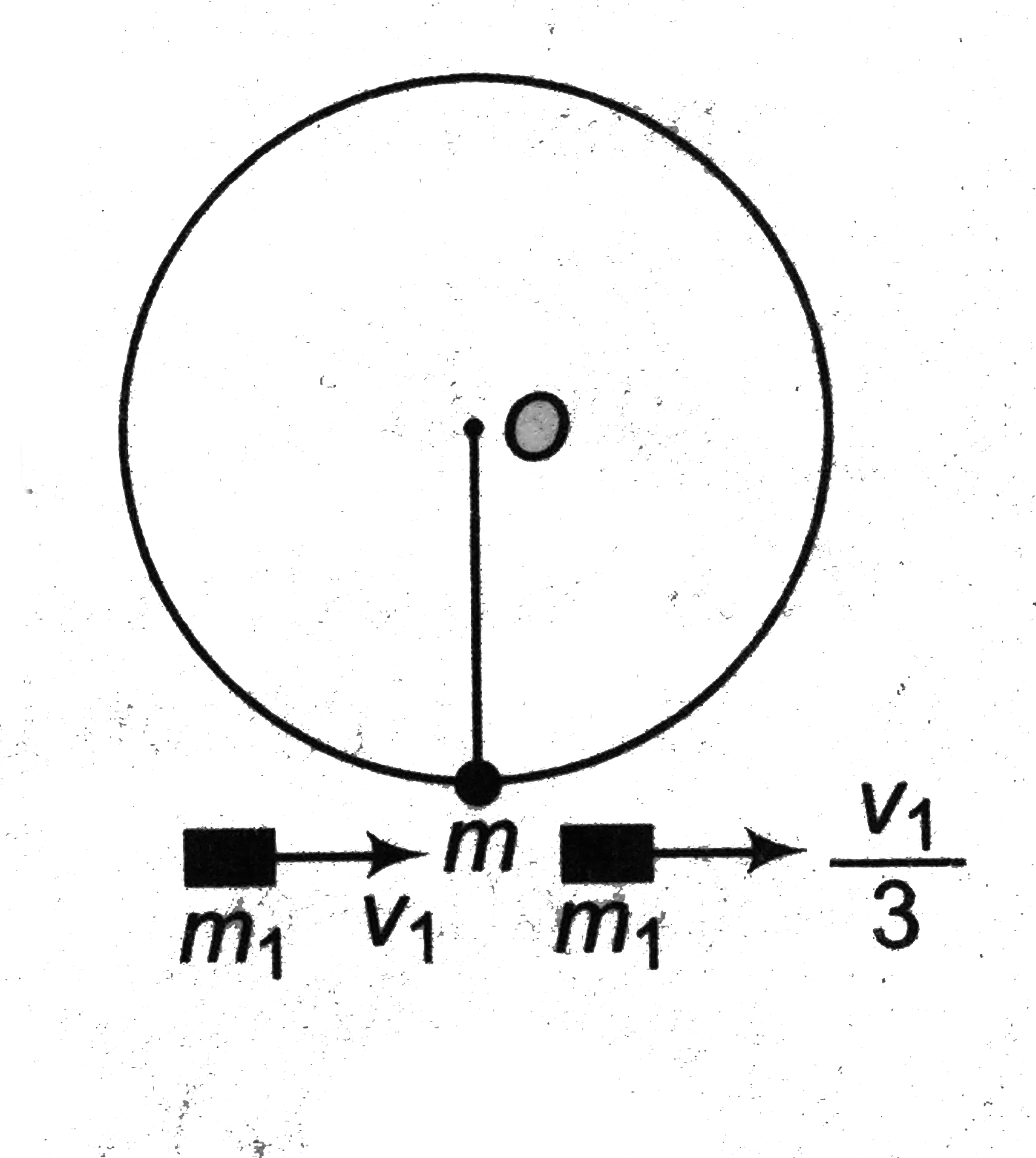
View SolutionA pendulum comsists of a wooden bob of mass m and length l. A bullet of mass m1 is fired towards the pendulum with a speed v1 and it emerges from the bob with speed v13. The bob just completes motion along a vertical circle. Then v1 is
 View Solution
View Solution