A potentiometer wire 10 long has a resistance of 40Ω. It is connected in series with a resistances box and a 2 v storage cell. If the potential gradient along the wire is 0.01Vm the resistance unplugged in the box is
260Ω
760Ω
960Ω
1060Ω
The correct Answer is:B
To solve the problem step by step, we will follow these calculations:
Step 1: Understand the given data
- Length of the potentiometer wire, L=10m
- Resistance of the potentiometer wire, Rwire=40Ω
- Voltage of the storage cell, V=2V
- Potential gradient, k=0.01V/m
Step 2: Calculate the potential difference across the potentiometer wire
The potential difference (VAB) across the length of the potentiometer wire can be calculated using the formula:
VAB=k×L
Substituting the values:
VAB=0.01V/m×10m=0.1V
Step 3: Calculate the current through the potentiometer wire
Using Ohm's law, the current (I) through the potentiometer wire can be calculated as:
I=VABRwire
Substituting the values:
I=0.1V40Ω=1400A
Step 4: Set up the equation for the total resistance in the circuit
The total resistance in the circuit (Rtotal) is the sum of the resistance of the potentiometer wire and the resistance in the box (R):
Rtotal=Rwire+R=40Ω+R
Step 5: Use the total voltage and current to find the total resistance
According to Ohm's law, the total voltage supplied by the cell is equal to the product of the current and the total resistance:
V=I×Rtotal
Substituting the known values:
2V=(1400A)×(40+R)
Step 6: Solve for R
Cross-multiplying gives:
2×400=40+R
800=40+R
Now, isolate R:
R=800−40=760Ω
Conclusion
The resistance unplugged in the box is R=760Ω.
---
- Length of the potentiometer wire, L=10m
- Resistance of the potentiometer wire, Rwire=40Ω
- Voltage of the storage cell, V=2V
- Potential gradient, k=0.01V/m
The potential difference (VAB) across the length of the potentiometer wire can be calculated using the formula:
VAB=k×L
Substituting the values:
VAB=0.01V/m×10m=0.1V
Using Ohm's law, the current (I) through the potentiometer wire can be calculated as:
I=VABRwire
Substituting the values:
I=0.1V40Ω=1400A
The total resistance in the circuit (Rtotal) is the sum of the resistance of the potentiometer wire and the resistance in the box (R):
Rtotal=Rwire+R=40Ω+R
According to Ohm's law, the total voltage supplied by the cell is equal to the product of the current and the total resistance:
V=I×Rtotal
Substituting the known values:
2V=(1400A)×(40+R)
Cross-multiplying gives:
2×400=40+R
800=40+R
Now, isolate R:
R=800−40=760Ω
The resistance unplugged in the box is R=760Ω.
Similar Questions
A potentiometer wire is 10 m long and has a resistance of 18Ω. It is connected to a battery of emf 5 V and internal resistance 2Ω. Calculate the potential gradient along the wire.
View SolutionA potentiometer wire of length 10 m and resistance 10Ω per meter is connected in serice with a resistance box and a 2 volt battery. If a potential difference of 100 mV is balanced across the whole length of potentiometer wire, then then the resistance introduce introduced in the resistance box will be
View Solution
Knowledge Check
A potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
A790ΩB890ΩC990ΩD1090ΩThe potentiometer wire of length 200cm has a resistance of 20Ω. It is connected in series with a resistance 10Ω and an accumulator of emf 6V having negligible internal resistance. A source of 2.4V is balanced against length 1 of the potentiometer wire. Find the length l of the potentiometer wire. Find the length l
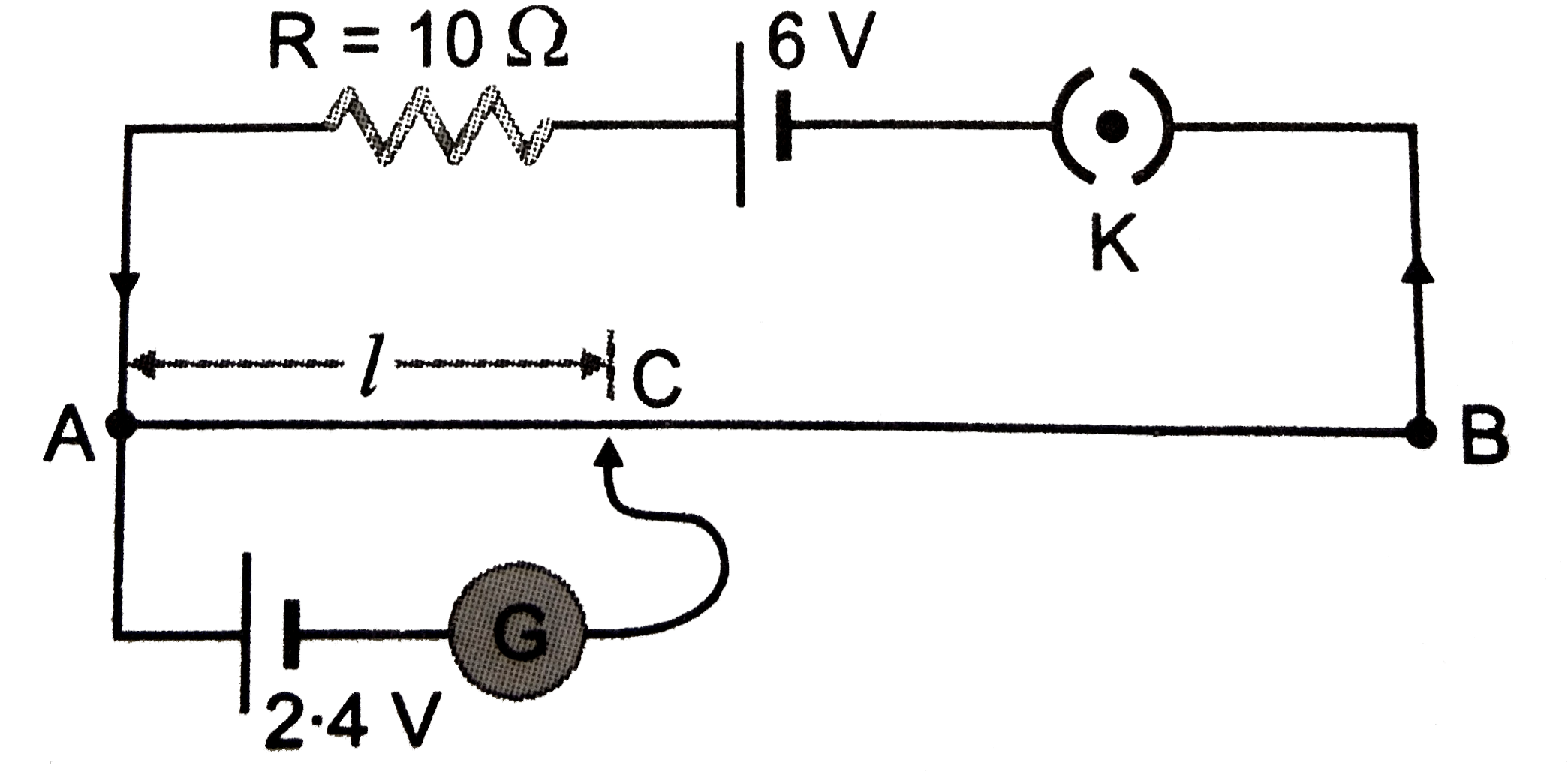 A100cmB120cmC110cmD140cm
A100cmB120cmC110cmD140cmA potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance and a cell of emf 2V and of negligible interal resistance. A source of emf 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of external resistance?
A790ΩB890ΩC990ΩD1090Ω
A potentiometer wire has resistance 40Ω and its length is 10m. It is connected by a resistance of 760Ω in series if emf of battery is 2V then potential gradient is:-
View SolutionA potentiometer wire of length 1 m has a resistance of 10Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and negligible resistance. A source of emf 10 mV is balanced against a length of 40cm of the potentiometer wire. What is the value of R?
View SolutionA potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf
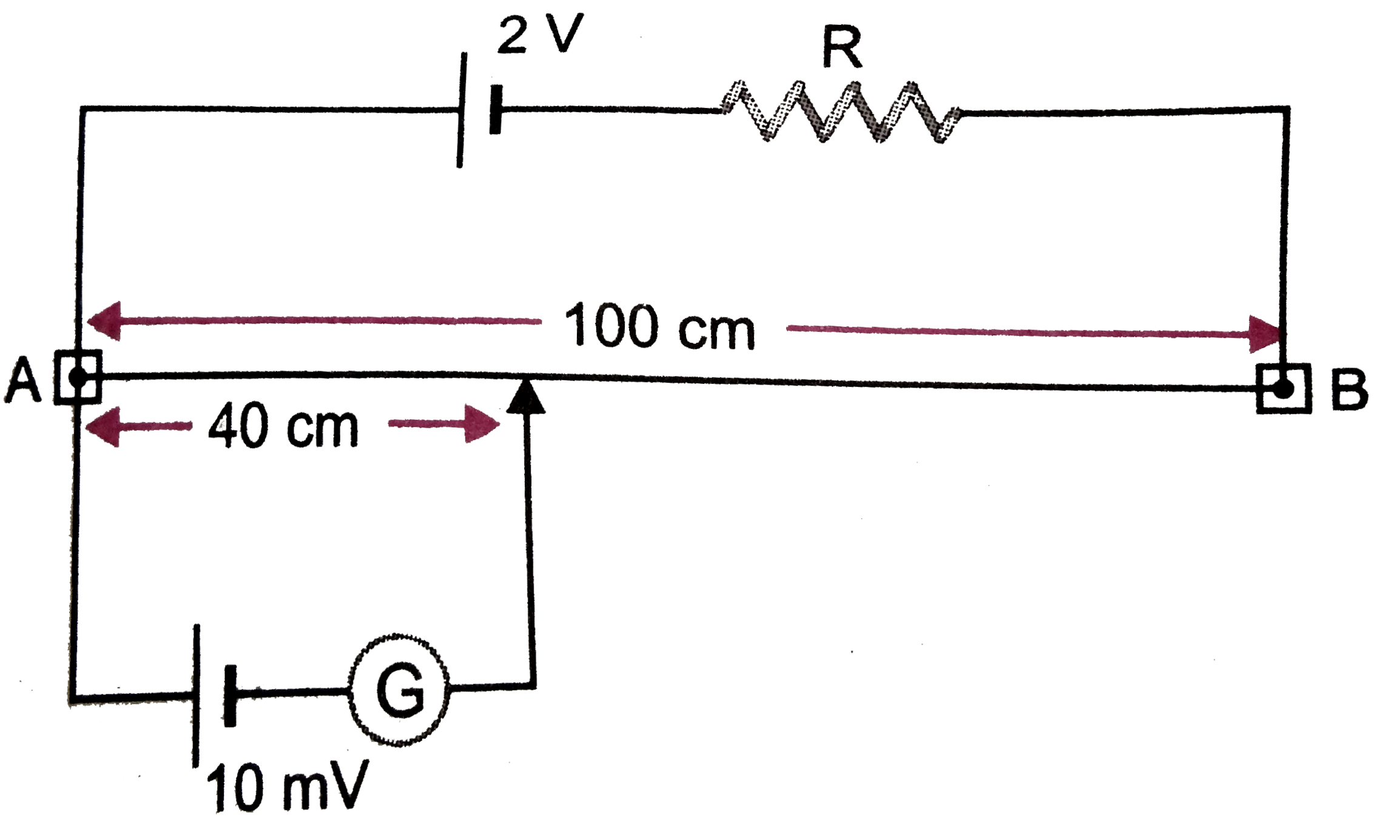
of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?
View SolutionA potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?
View Solution