A 10 g bullet moving directly upward at 1000ms−1 strikes and passes through the center of mass of a 10 kg block initially at rest. The bullet emerges from the block moving directly upwards at 400ms−1 . What will be the velocity of the block just after the bullet comes out of it ?
1ms−1
0.4ms−1
1.4ms−1
0.6ms−1
The correct Answer is:D
To solve the problem, we will use the principle of conservation of momentum. The momentum before the bullet strikes the block must equal the momentum after the bullet passes through the block.
1. Identify the given values:
- Mass of the bullet, mb=10g=10×10−3kg
- Initial velocity of the bullet, ub=1000m/s
- Final velocity of the bullet after passing through the block, vb=400m/s
- Mass of the block, mblock=10kg
- Initial velocity of the block, ublock=0m/s (since it is at rest)
2. Write the conservation of momentum equation:
The total momentum before the collision equals the total momentum after the collision.
mb⋅ub+mblock⋅ublock=mb⋅vb+mblock⋅vblock
3. Substitute the known values into the equation:
(10×10−3kg)⋅(1000m/s)+(10kg)⋅(0m/s)=(10×10−3kg)⋅(400m/s)+(10kg)⋅vblock
4. Calculate the left side of the equation:
10×10−3⋅1000=10kg m/s
5. Calculate the right side of the equation:
10×10−3⋅400=4kg m/s
So the equation becomes:
10=4+10⋅vblock
6. Rearranging the equation to solve for vblock:
10−4=10⋅vblock
6=10⋅vblock
vblock=610=0.6m/s
7. Conclusion:
The velocity of the block just after the bullet comes out of it is 0.6m/s.
- Mass of the bullet, mb=10g=10×10−3kg
- Initial velocity of the bullet, ub=1000m/s
- Final velocity of the bullet after passing through the block, vb=400m/s
- Mass of the block, mblock=10kg
- Initial velocity of the block, ublock=0m/s (since it is at rest)
The total momentum before the collision equals the total momentum after the collision.
mb⋅ub+mblock⋅ublock=mb⋅vb+mblock⋅vblock
(10×10−3kg)⋅(1000m/s)+(10kg)⋅(0m/s)=(10×10−3kg)⋅(400m/s)+(10kg)⋅vblock
10×10−3⋅1000=10kg m/s
10×10−3⋅400=4kg m/s
So the equation becomes:
10=4+10⋅vblock
10−4=10⋅vblock
6=10⋅vblock
vblock=610=0.6m/s
The velocity of the block just after the bullet comes out of it is 0.6m/s.
Similar Questions
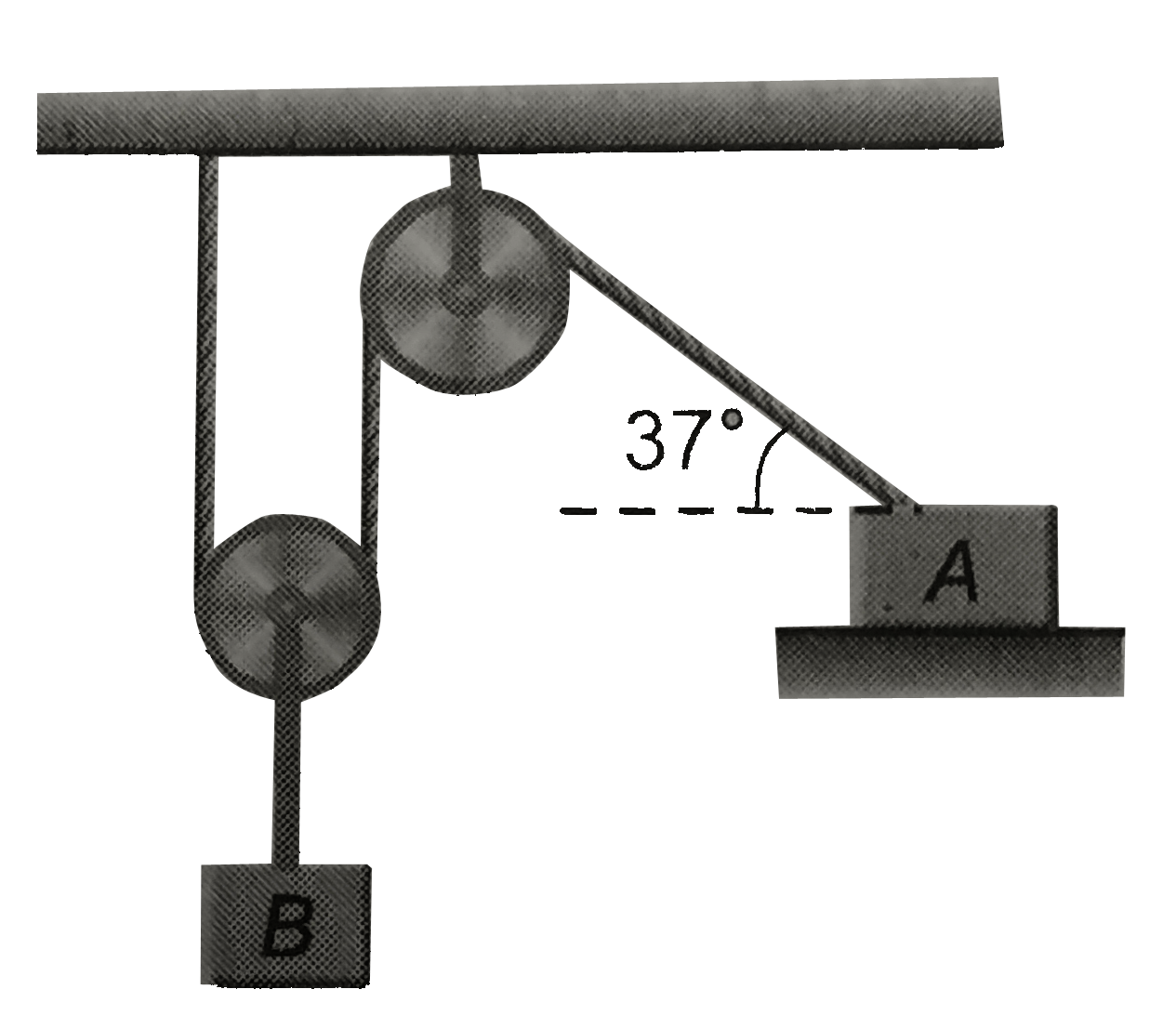
In the figure shown the block B moves with , velocity 10ms−1. The velocity of A in the position shown is
View SolutionA bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View SolutionA bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bulet emerges with speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction cioefficient between the block and the surface figure.

View SolutionA bullet of mass 0.005 kg moving with a speed of 200 ms−1 enters a heavy wooden block and is stopped after a distance of 50 cm. What is the average force exerted by the block on the bullet?
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View SolutionA bullet of mass 5 g is fired at a velocity of 900ms−1 from a rifle of mass 2.5 kg. What is the recoil velocity of the rifle?
View SolutionA bullet initially moving with a velocity 20 m s−1 strikes a target and comes to rest after penetrating a distance 10 cm in the target. Calculate the retardation caused by the target.
View SolutionA bullet moving with a velocity of 30√2ms−1 is fired into a fixed target. It penetrated into the target to the extent of s metres. If the same bullet is fired into a target of thickness s2 metres and of the same material with the same velocity, then the bullet comes out of the target with velocity
View SolutionA 4.00g bullet travelling horizontally with a velocity of magnitude 500m/s is fired into a wooden block with a mass of 1.00kg, initially at rest on a level surface. The bullet passes through the block and emerges with speed 100m/s. The block slides a distance of 0.30m along the surface from its initial position.
(a) What is the coefficient of kinetic friction between block and surface?
(b) What is the decrease in kinetic energy of the bullet?
(c) What is the kinetic energy of the block at the instant after the bullet has passed through it? Neglect friction during collision of bullet with the block.
View SolutionA bullet of mass 0.012 kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View Solution
