Question

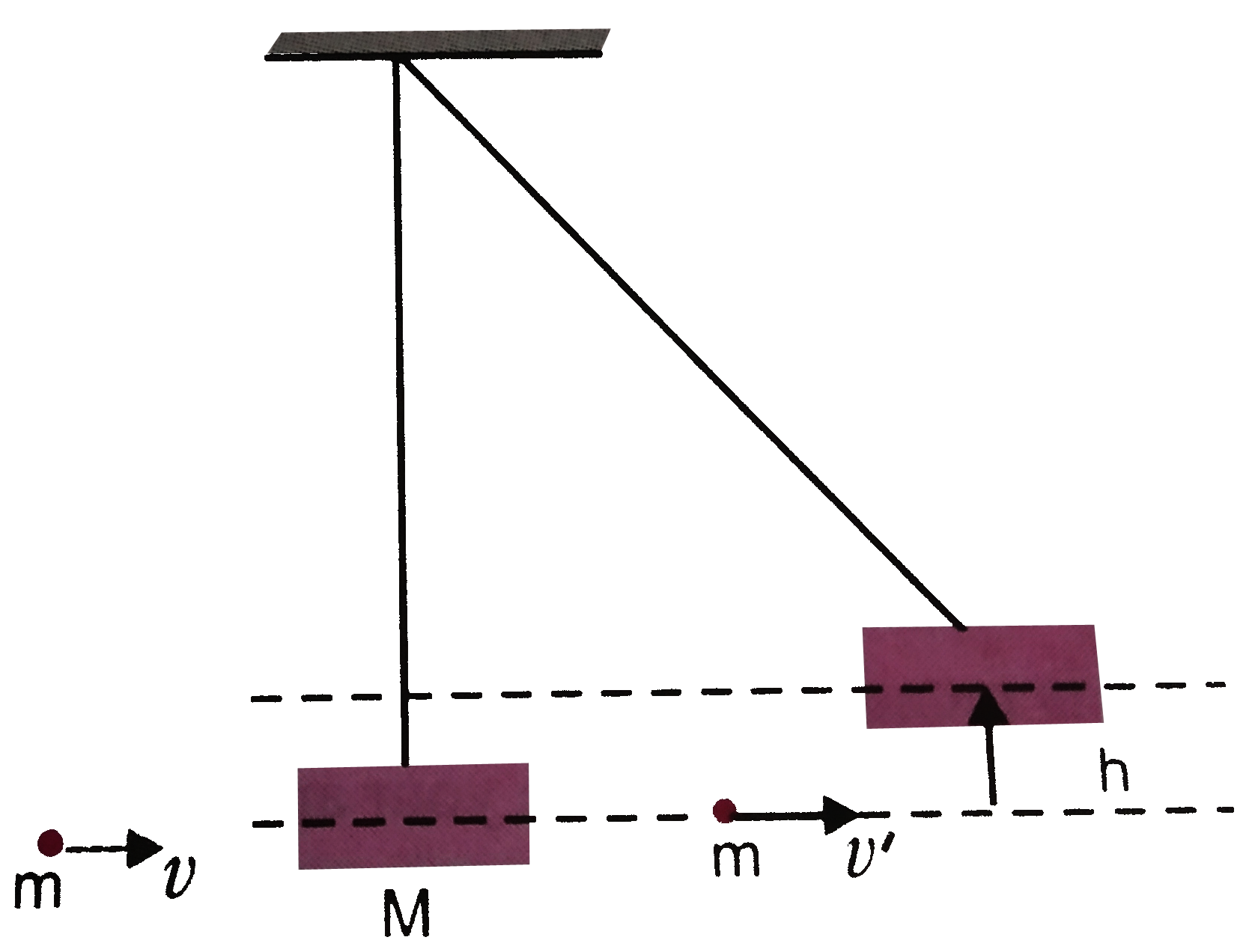
A bullet of mass 0.012 kg and horizontal speed $70m{s}^{-1}$ strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.

Explanation

To solve the problem step by step, we will follow these steps:

Step 1: Calculate the initial momentum of the bullet and the block.
The initial momentum of the bullet can be calculated using the formula:
\( \text{Initial Momentum} = \text{mass of bullet} \times \text{velocity of bullet} \)
Given:
- Mass of bullet, \( m_b = 0.012 \, \text{kg} \)
- Velocity of bullet, \( v_b = 70 \, \text{m/s} \)

Calculating the initial momentum:
\( \text{Initial Momentum} = 0.012 \, \text{kg} \times 70 \, \text{m/s} = 0.84 \, \text{kg m/s} \)

Step 2: Apply the conservation of momentum to find the final velocity \( V_0 \).
The block is initially at rest, so its momentum is zero. The total initial momentum before the collision is equal to the total final momentum after the collision:
\( \text{Initial Momentum} = \text{Final Momentum} \)
\( 0.84 \, \text{kg m/s} = (m_b + m_w) \times V_0 \)
Where:
- Mass of the block, \( m_w = 0.4 \, \text{kg} \)
- Total mass after collision, \( m_b + m_w = 0.012 \, \text{kg} + 0.4 \, \text{kg} = 0.412 \, \text{kg} \)

Now, substituting the values:
\( 0.84 = 0.412 \times V_0 \)
Solving for \( V_0 \):
\( V_0 = \frac{0.84}{0.412} \approx 2.04 \, \text{m/s} \)

Step 3: Calculate the height \( h \) to which the block rises using energy conservation.
The kinetic energy of the system after the collision will be converted into potential energy at the maximum height:
\( \text{Kinetic Energy} = \text{Potential Energy} \)
\( \frac{1}{2} (m_b + m_w) V_0^2 = (m_b + m_w) g h \)
Cancelling the mass from both sides:
\( \frac{1}{2} V_0^2 = g h \)
Solving for \( h \):
\( h = \frac{V_0^2}{2g} \)
Using \( g \approx 9.81 \, \text{m/s}^2 \):
\( h = \frac{(2.04)^2}{2 \times 9.81} \approx \frac{4.1616}{19.62} \approx 0.2123 \, \text{m} \)

Step 4: Calculate the heat produced in the block.
The heat produced can be calculated as the loss of kinetic energy during the collision:
\( \text{Heat Produced} = \text{Initial Kinetic Energy} - \text{Final Kinetic Energy} \)
Calculating the initial kinetic energy of the bullet:
\( \text{Initial Kinetic Energy} = \frac{1}{2} m_b v_b^2 = \frac{1}{2} \times 0.012 \times (70)^2 = \frac{1}{2} \times 0.012 \times 4900 = 29.4 \, \text{J} \)
Calculating the final kinetic energy of the combined mass:
\( \text{Final Kinetic Energy} = \frac{1}{2} (m_b + m_w) V_0^2 = \frac{1}{2} \times 0.412 \times (2.04)^2 = \frac{1}{2} \times 0.412 \times 4.1616 \approx 0.857 \, \text{J} \)
Now, calculating the heat produced:
\( \text{Heat Produced} = 29.4 \, \text{J} - 0.857 \, \text{J} \approx 28.54 \, \text{J} \)

Final Answers:
- Height to which the block rises: \( h \approx 0.2123 \, \text{m} \)
- Heat produced in the block: \( \approx 28.54 \, \text{J} \)